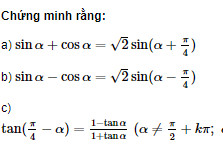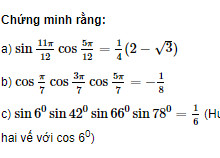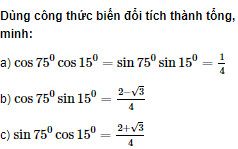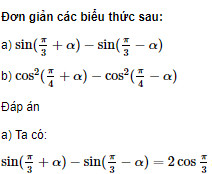Giải bài 35 trang 207 SGK Đại số 10 Nâng cao
Chia sẻ trang này
Tính:
- Bài học cùng chủ đề:
- Bài 36 trang 207 SGK Đại số 10 Nâng cao
- Bài 37 trang 207 SGK Đại số 10 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Biết \(\sinα -\cosα =m\), hãy tính \(si{n^3}\alpha {\rm{ }} - {\rm{ }}co{s^3}\alpha \)
Đáp án
Ta có:
\(si{n^3}\alpha {\rm{ }} - {\rm{ }}co{s^3}\alpha \)
\( = {\rm{ }}\left( {sin\alpha {\rm{ }}-{\rm{ }}cos\alpha } \right)(si{n^2}\alpha {\rm{ }} + {\rm{ }}sin\alpha {\rm{ }}cos\alpha {\rm{ }} + {\rm{ }}co{s^2}\alpha )\)
\(= m(1 + sinα cosα)\) (1)
Từ \(\sinα – \cosα = m ⇒ 1 - 2\sinα \cosα = m^2\)
⇒ \(\sin \alpha \,\cos \alpha = {{1 - {m^2}} \over 2}\,\,\,\,\,\,\,(2)\)
Thay (2) vào (1) ta được:
\({\sin ^3}\alpha - {\cos ^3}\alpha = m(1 + {{1 - {m^2}} \over 2}) = {m \over 2}(3 - {m^2})\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. mệnh đề - tập hợp
- Chương ii. hàm số bậc nhất và bậc hai
- Chương iii. phương trình và hệ phương trình
- Chương iv. bất phương trình và hệ bất phương trình
- Chương v. thống kê
- Chương vi. góc lượng giác và công thức lượng giác
- Ôn tập cuối năm đại số
- Chương i. vectơ
- Chương ii. tích vô hướng của hai vectơ và ứng dụng
- Chương iii. phương pháp tọa độ trong mặt phẳng
- Ôn tập cuối năm hình học
