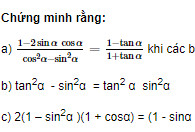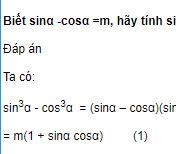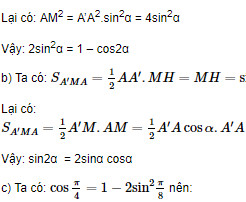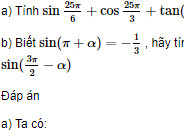
Giải bài 29 trang 206 SGK Đại số 10 Nâng cao

Chia sẻ trang này

Hãy tính các giá trị lượng giác của góc -750

Biết tan 15⁰ = \(2 - \sqrt 3 \) .

Hãy tính các giá trị lượng giác của góc -75⁰

Đáp án

Từ tan 15⁰ = \(2 - \sqrt 3 \) , suy ra:

\(\eqalign{
& {\cos ^2}{15^0} = {1 \over {1 + (2 - \sqrt 3 )^2}} = {{2 + \sqrt 3 } \over 4} \cr
& \cos {15^0} = {{\sqrt {2 + \sqrt 3 } } \over 2} = {{\sqrt 3 + 1} \over {2\sqrt 2 }} \cr
& \sin {15^0} = {{\sqrt 3 - 1} \over {2\sqrt 2 }} \cr} \)

Do 75⁰ = 90⁰ – 15⁰nên:

\(\eqalign{
& \cos {(-75^0)} = \cos {75^0} = \sin {15^0} = {{\sqrt 3 - 1} \over {2\sqrt 2 }} \cr
& \sin ( - {75^0}) = - \sin ({90^0} - {15^0}) \cr&= - \cos {15^0} = - {{\sqrt 3 + 1} \over {2\sqrt 2 }} \cr
& \tan ( - {75^0}) = - \cot {15^0} = {1 \over {\sqrt 3 - 2}} = - (\sqrt 3 + 2) \cr
& \cot ( - {75^0}) = - \tan {15^0} = \sqrt 3 - 2 \cr} \)

Trên đây là bài học "Giải bài 29 trang 206 SGK Đại số 10 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 2 lớp 10" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 10 của dayhoctot.com.