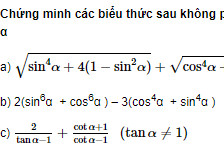
Giải bài 19 trang 200 SGK Đại số 10 Nâng cao

Bài trước
Bài sau  

Đơn giản các biểu thức

Đơn giản các biểu thức

a) \(\sqrt {{{\sin }^4}\alpha  + {{\sin }^2}\alpha {{\cos }^2}\alpha } \)

b) \({{1 - \cos \alpha } \over {{{\sin }^2}\alpha }} - {1 \over {1 + \cos \alpha }}\,\,(\sin \alpha  \ne 0)\)

c) \({{1 - {{\sin }^2}\alpha {{\cos }^2}\alpha } \over {{{\cos }^2}\alpha }} - {\cos ^2}\alpha \,\,\,(cos\alpha  \ne 0)\)

Đáp án

a) Ta có:

\(\eqalign{
& \sqrt {{{\sin }^4}\alpha + {{\sin }^2}\alpha {{\cos }^2}\alpha } = \sqrt {{{\sin }^2}\alpha ({{\sin }^2}\alpha + {{\cos }^2}\alpha )} \cr
& = \sqrt {{{\sin }^2}\alpha } = |\sin \alpha | \cr} \)

b) Ta có:

\(\eqalign{
& {{1 - \cos \alpha } \over {{{\sin }^2}\alpha }} - {1 \over {1 + \cos \alpha }}= {{1 - \cos \alpha } \over {1 - {{\cos }^2}\alpha }} - {1 \over {1 + \cos \alpha }} \cr
& = {1 \over {1 + \cos \alpha }} - {1 \over {1 + \cos \alpha }} = 0 \cr} \)

c) Ta có:

\(\eqalign{
& {{1 - {{\sin }^2}\alpha{{\cos }^2}\alpha} \over {{{\cos }^2}\alpha}} - {\cos ^2}\alpha\cr&= {1 \over {{{\cos }^2}\alpha }} - {\sin ^2}\alpha - {\cos ^2}\alpha \cr
& = {1 \over {{{\cos }^2}\alpha }} - 1 = {\tan ^\alpha } \cr} \)

 

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 10

Bài học nổi bật nhất

Đề thi lớp 10 mới cập nhật