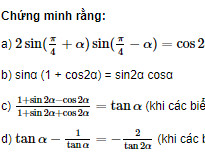Giải bài 48 trang 215 SGK Đại số 10 Nâng cao
Chứng minh rằng:
- Bài học cùng chủ đề:
- Bài 49 trang 215 SGK Đại số 10 Nâng cao
- Bài 50 trang 215 SGK Đại số 10 Nâng cao
- Bài 51 trang 216 SGK Đại số 10 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Chứng minh rằng: \(\cos {{2\pi } \over 7} + \cos {{4\pi } \over 7} + \cos {{6\pi } \over 7} = - {1 \over 2}\)
Hướng dẫn: Nhân vế trái với \({\pi \over 7}\) (hoặc \({{2\pi } \over 7}\) ) rồi sử dụng công thức biến đổi tích thành tổng.
Đáp án
Đặt \(A = \cos {{2\pi } \over 7} + \cos {{4\pi } \over 7} + \cos {{6\pi } \over 7}\) , ta có:
\(\eqalign{
& 2A\sin {\pi \over 7} = 2\cos {{2\pi } \over 7}\sin {\pi \over 7} + 2\cos {{4\pi } \over 7}\sin {\pi \over 7}\cr& + 2\cos {{6\pi } \over 7}\sin {\pi \over 7} \cr
& = (\sin {{3\pi } \over 7} - \sin {\pi \over 7}) + (\sin {{5\pi } \over 7} - \sin {{3\pi } \over 7})\cr&+ (\sin {{7\pi } \over 7} - \sin {{5\pi } \over 7}) = - sin{\pi \over 7} \cr
& \Rightarrow A = - {1 \over 2} \cr} \)
- Chương i. mệnh đề - tập hợp
- Chương ii. hàm số bậc nhất và bậc hai
- Chương iii. phương trình và hệ phương trình
- Chương iv. bất phương trình và hệ bất phương trình
- Chương v. thống kê
- Chương vi. góc lượng giác và công thức lượng giác
- Ôn tập cuối năm đại số
- Chương i. vectơ
- Chương ii. tích vô hướng của hai vectơ và ứng dụng
- Chương iii. phương pháp tọa độ trong mặt phẳng
- Ôn tập cuối năm hình học