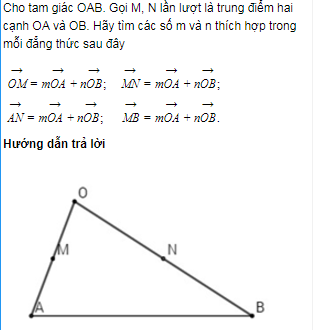
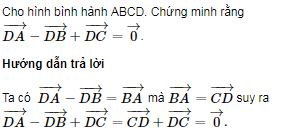Giải bài 12 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Bài trước
Bài sau  

Cho tam giác đều ABC nội tiếp đường tròn tâm O. a) Hãy xác định các điểm M, N, P sao cho

Bài 12. Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\).

a)  Hãy xác định các điểm \(M, N, P\) sao cho

\(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \,;\,\,\,\overrightarrow {ON}  = \overrightarrow {OB}  + \overrightarrow {OC} \,;\,\,\,\overrightarrow {OP}  = \overrightarrow {OC}  + \overrightarrow {OA} \)

b) Chứng minh rằng \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \).

Hướng dẫn trả lời

 

a) Theo quy tắc hình bình hành, ta có \(AOBM\) là hình bình hành.

Ta có \(AB, OM\) cắt nhau tại trung điểm mỗi đường, gọi \(I\) là trung điểm \(AB\) thì \(OI = IM\). \(O\) là trọng tâm tam giác \(ABC\) nên \(OC = 2 OI = OM\).

Do đó \(O\) là trung điểm của \(MC\), tức là \(MC\) là đường kính của đường tròn.

Vậy điểm \(M\) là điểm sao cho \(CM\) là đường kính của đường tròn tâm \(O\).

Tương tự, ta cũng có \(N, P\) thuộc đường tròn \((O)\) sao cho \(AN, BP\) là đường kính của đường tròn \((O)\).

b) \(O\) là trung điểm của \(MC\) nên \(\overrightarrow {OM}  + \overrightarrow {OC}  = \overrightarrow 0 \), mà \(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \) suy ra \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \) 

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 10

Bài học nổi bật nhất

Đề thi lớp 10 mới cập nhật