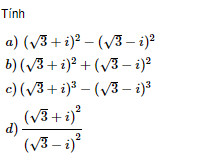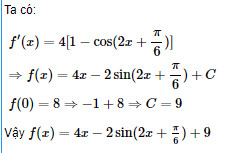
Giải câu 9 trang 212 SGK Giải tích 12 Nâng cao

Chia sẻ trang này

a) Vẽ đồ thị của các hàm số y = 2^x; \(y = {(\sqrt 2 )^x}\) và \(y = {(\sqrt 3 )^x}\) trên cùng một mặt phẳng tọa độ,

Hãy nêu nhận xét về trị trí tương đối của ba đồ thị hàm số đó.

b) Vẽ đồ thị hàm số y = log₃x.

Từ đó suy ra đồ thị của hàm số y = 2 + log₃x và đồ thị của hàm số y = log₃(x + 2)

Giải

a) Với x > 0 thì \({2^x} > {(\sqrt 3 )^x} > {(\sqrt 2 )^x}\)

nên x > 0 đồ thị y = 2^x nằm phía trên đồ thị \(y = {(\sqrt 3 )^x}\) và đồ thị \(y = {(\sqrt 3 )^x}\) nằm phía trên đồ thị \(y = {(\sqrt 2 )^x}\)

Với x < 0 thì \({2^x} < {(\sqrt 3 )^x} < {(\sqrt 2 )^x}\)

nên với x < 0 thì y = 2^x nằm phía dưới đồ thị \(y = {(\sqrt 3 )^x}\) và đồ thị \(y = {(\sqrt 3 )^x}\) nằm phía dưới đồ thị \(y = {(\sqrt 2 )^x}\)

b) Đồ thị y = 2 + log₃x có được bằng cách tịnh tiến lên 2 đơn vị của đồ thị y = log₃x

Đồ thị y = log₃(x + 2) có được bằng cách tịnh tiến sang trái 2 đơn vị của đồ thị y = log₃x

dayhoctot.com

Trên đây là bài học "Giải câu 9 trang 212 SGK Giải tích 12 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 12" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 12 của dayhoctot.com.