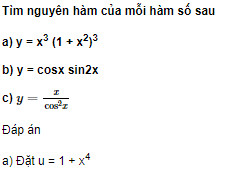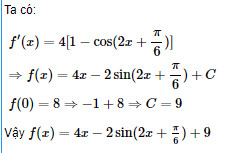Giải câu 5 trang 212 SGK Giải tích 12 Nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau:
- Bài học cùng chủ đề:
- Câu 6 trang 212 SGK Giải tích 12 Nâng cao
- Câu 7 trang 212 SGK Giải tích 12 Nâng cao
- Câu 8 trang 212 SGK Giải tích 12 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = {1 \over {\sqrt { - {x^2} + x + 6} }}\) trên đoạn [0, 1]
Giải
Xét hàm số g(x) = -x2 + x + 6 với x ∈ [0, 1)
Ta có:
\(\eqalign{
& g'(x) = - 2x + 1 \cr
& g'(x) = 0 \Leftrightarrow x = {1 \over 2} \cr} \)
\(\eqalign{
& g(0) = 6;\,\,\,g({1 \over 2}) = {{25} \over 4};\,\,\,g(1) = 6 \cr
& \mathop {\min }\limits_{x \in {\rm{[}}0,1{\rm{]}}} (x) = 6;\,\,\,\mathop {\max }\limits_{x \in {\rm{[}}0,1{\rm{]}}} (x) = {{25} \over 4} \cr} \)
\(\eqalign{
& \Rightarrow 6 \le g(x) \le {{25} \over 4}\,\,\,(\forall x \in {\rm{[}}0,1{\rm{]}}) \cr
& \Rightarrow {2 \over 5} \le f(x) = {1 \over {\sqrt {g(x)} }} \le {{\sqrt 6 } \over 6} \cr} \)
Vậy \(\mathop {\max}\limits_{x \in [0,1{\rm{]}}} (fx) = {{\sqrt 6 } \over 6};\,\,\,\mathop {\min }\limits_{x \in [0,1{\rm{]}}} (fx) = {2 \over 5}\)
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học