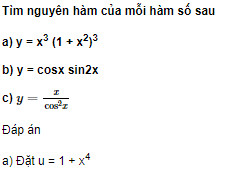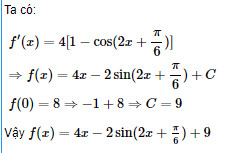Giải câu 6 trang 212 SGK Giải tích 12 Nâng cao
Hãy tính:
- Bài học cùng chủ đề:
- Câu 7 trang 212 SGK Giải tích 12 Nâng cao
- Câu 8 trang 212 SGK Giải tích 12 Nâng cao
- Câu 9 trang 212 SGK Giải tích 12 Nâng cao
- Ngữ pháp tiếng anh hay nhất
a) Cho \(P(x) = {{{4^x}} \over {{4^x} + 2}}\) và hai số a, b thỏa mãn a + b = 1
Hãy tính P(a) + P(b)
b) Hãy so sánh \(A = \root 3 \of {18} \) và \(B = {({1 \over 6})^{\log _62 - {1 \over 2}\log _{\sqrt 6 }5}}\)
Giải
a) Ta có:
\(\eqalign{
& p(a) + p(b) = {{{4^a}} \over {{4^a} + 2}} + {{{4^b}} \over {{4^b} + 2}} \cr
& = {{{4^a}({4^b} + 2) + {4^b}({4^a} + 2)} \over {({4^a} + 2)({4^b} + 2)}} = {{{{2.4}^{a + b}} + 2({4^a} + {4^b})} \over {{4^{a + b}} + 4 + 2({4^a} + {4^b})}} \cr
& = {{8 + 2({4^a} + {4^b})} \over {8 + 2({4^a} + {4^b})}} = 1 \cr} \)
b) Ta có:
\(\eqalign{
& B = {({1 \over 6})^{\log _62 - {1 \over 2}\log _{\sqrt 6 }5}} ={6^{-\log _62 + \log _{ 6 }5}}= {6^{{{\log }_6}{5 \over 2}}} = {5 \over 2} \cr
& {A^3} = 18 > {({5 \over 2})^3}=B^3 \cr} \)
Suy ra A > B
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học