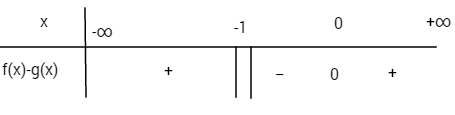Giải bài 68 trang 61 SGK giải tích 12 nâng cao
Chia sẻ trang này
Chứng minh các bất đẳng thức sau:
- Bài học cùng chủ đề:
- Bài 69 trang 61 SGK giải tích 12 nâng cao
- Bài 70 trang 61 SGK giải tích 12 nâng cao
- Bài 71 trang 62 SGK giải tích 12 nâng cao
- Ngữ pháp tiếng anh hay nhất
Bài 68. Chứng minh các bất đẳng thức sau:
a) \(\tan x > x,\,\forall x \in \left( {0;{\pi \over 2}} \right)\);
b) \(\tan x > x + {{{x^3}} \over 3},\,\forall x \in \left( {0;{\pi \over 2}} \right)\)
Hướng dẫn: a) Chứng minh rằng hàm số: \(f\left( x \right) = \tan x - x\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\)
Giải
a) Hàm số \(f\left( x \right) = \tan x - x\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và có đạo hàm \(f'\left( x \right) = {1 \over {{{\cos }^2}x}} - 1 > 0\,\,\forall x\left( {0;{\pi \over 2}} \right)\)
Do đó hàm số \(f\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\)
Từ đó: \(f\left( x \right) > f\left( 0 \right)\forall x \in \left( {0;{\pi \over 2}} \right) \Leftrightarrow \tan x - x > 0\forall x \in \left( {0;{\pi \over 2}} \right)\)
b) Hàm số \(f\left( x \right) = \tan x - x - {{{x^3}} \over 3}\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và có đạo hàm \(f'\left( x \right) = {1 \over {{{\cos }^2}x}} - 1 = {\tan ^2}x - {x^2} > 0\,\,\forall x\left( {0;{\pi \over 2}} \right)\) (suy ra từ a)).
Do đó hàm số \(f\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và khi đó
\(f\left( x \right) = f\left( 0 \right) = 0\,\,\forall x \in \left( {0;{\pi \over 2}} \right) \Rightarrow \tan x > x + {{{x^3}} \over 3}\,\,\forall x \in \left( {0;{\pi \over 2}} \right)\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học
