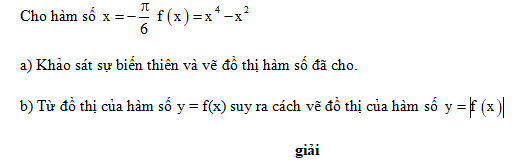Giải bài 66 trang 58 SGK giải tích 12 nâng cao
Tìm các hệ số a, b sao cho parabol tiếp xúc với hypebol tại điểm
Bài 66. Tìm các hệ số \(a, b\) sao cho parabol \(y = 2{x^2} + ax + b\) tiếp xúc với hypebol \(y = {1 \over x}\) tại điểm \(M\left( {{1 \over 2};2} \right)\)
Giải
Giả sử \(f\left( x \right) = 2{x^2} + ax + b;\,g\left( x \right) = {1 \over x}\)
Parabol tiếp xúc với hypebol tại \(M\left( {{1 \over 2};2} \right)\) khi và chỉ khi
\(\left\{ \matrix{
f\left( {{1 \over 2}} \right) = g\left( {{1 \over 2}} \right) = 2 \hfill \cr
f'\left( {{1 \over 2}} \right) = g'\left( {{1 \over 2}} \right) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{1 \over 2} + {a \over 2} + b = 2 \hfill \cr
4.{1 \over 2} + a = - {1 \over {{{\left( {{1 \over 2}} \right)}^2}}} \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
a + 2b = 3 \hfill \cr
a + 2 = - 4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - 6 \hfill \cr
b = {9 \over 2} \hfill \cr} \right.\)
Trên đây là bài học "Giải bài 66 trang 58 SGK giải tích 12 nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 12" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 12 của dayhoctot.com.
Các bài học liên quan
Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhât.
Cho hàm số:
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
b) Chứng minh rằng phương trình f(x) =0 có ba nghiệm phân biệt.
Cho hàm số
a) Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu.
b) Chứng minh rằng nếu giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình: có ba nghiệm phân biệt.
c) Chứng minh rằng điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là:
Cho hàm số:
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn U của nó.
c) Gọi là đường thẳng đi qua điểm U và có hệ số góc m. Tìm các giá trị của m sao cho đường thẳng cắt đồ thị của hàm số đã cho tại ba điểm phân biệt.
Cho hàm số:
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.
b) Tìm các giá trị của m sao cho đồ thị của hàm số cắt trục hoành tại bốn điểm, tạo thành ba đoạn thẳng có độ dài bằng nhau.
Cho hàm số
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.
b) Từ đồ thị của hàm số y = f(x) suy ra cách vẽ đồ thị của hàm số
Cho hàm số:
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1.
b) Chứng minh rằng với mọi , các đường cong đều đi qua hai điểm cố định A và B.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 12