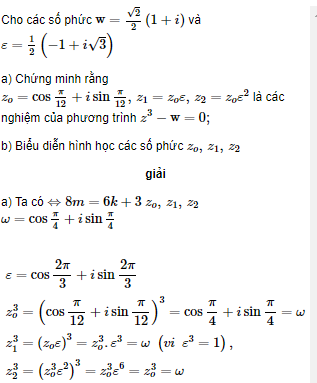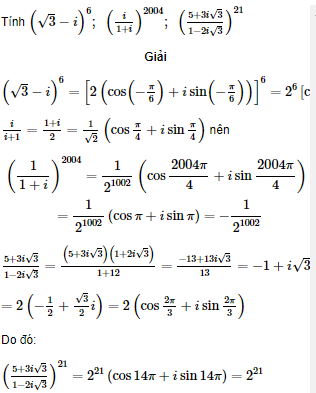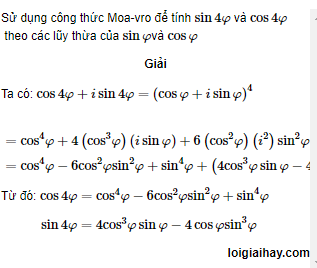
Giải bài 22 trang 197 SGK Đại số và Giải tích 12 Nâng cao

Chia sẻ trang này

Đố vui. Một học sinh kí hiệu một căn bậc hai của -1

Bài 22

Đố vui. Một học sinh kí hiệu một căn bậc hai của \(-1\) là \(\sqrt { - 1} \) và tính \(\sqrt { - 1} \).\(\sqrt { - 1} \) như sau:

a) Theo định nghĩa căn bậc hai của \(-1\) thì \(\sqrt { - 1} \).\(\sqrt { - 1} = - 1\) .

b) Theo tính chất của căn bậc hai ( tính của hai căn bậc hai của hai số bằng căn bậc hai của tích hai số đó ) thì \(\sqrt { - 1} .\sqrt { - 1} = \sqrt {\left( { - 1} \right).\left( { - 1} \right)} = \sqrt 1 = 1\)

Từ đó, học sinh đó suy ra \(-1 = 1\)

Hãy tìm điều sai trong lập luận trên.

Giải

Lập luận a) là đúng

Lập luận b) sai ở chỗ; nếu z₁ là một căn bậc hai của w₁, z₂ là một căn bậc hai của w₂ thì \({z_1}{z_2}\) là một trong hai căn bậc hai của \({{\rm{w}}_1}{{\rm{w}}_2}\); vậy ở đây \(\sqrt { - 1} \).\(\sqrt { - 1} \) chỉ là một căn bậc hai của \(\left( { - 1} \right)\left( { - 1} \right) = 1\) (để ý rằng có hai căn bậc hai của 1 là 1 và -1), các kí hiệu \(\sqrt {\left( { - 1} \right)\left( { - 1} \right)} \) và \(\sqrt 1 \) chưa xác định.

Trên đây là bài học "Giải bài 22 trang 197 SGK Đại số và Giải tích 12 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 12" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 12 của dayhoctot.com.