Giải bài 18 trang 59 SGK Hình học 12 Nâng cao
Chia sẻ trang này
Cho điểm A nằm trong mặt cầu S. Chứng minh rằng các đường thẳng đi qua A tiếp xúc với mặt cầu S luôn nằm trên một mặt nón xác định.
- Bài học cùng chủ đề:
- Bài 19 trang 60 SGK Hình học 12 Nâng cao
- Bài 20 trang 60 SGK Hình học 12 Nâng cao
- Bài 21 trang 60 SGK Hình học 12 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Bài 18. Cho điểm \(A\) nằm trong mặt cầu \(S\). Chứng minh rằng các đường thẳng đi qua \(A\) tiếp xúc với mặt cầu \(S\) luôn nằm trên một mặt nón xác định.
Giải
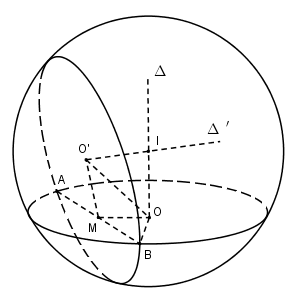
Giả sử \(Al\) là một tiếp tuyến của mặt cầu \(S(I;R)\) với tiếp điểm là \(M\). Khi đó nếu \(\Delta \) là đường thẳng \(AI\) và \(\alpha \) là góc giữa đường thẳng \(Al\) và \(\Delta \) thì \(\alpha = \widehat {MAI}\).
Ta có: \(9\sin \alpha = {{MI} \over {IA}} = {R \over {IA}}\), suy ra góc \(\alpha \) không đổi. Vậy \(Al\) là đường sinh của mặt nón \((N)\) có đỉnh \(A\) và góc ở đỉnh là \(2\alpha \).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học
