Giải bài 1 trang 45 SGK Hình học 12 Nâng cao
Trong không gian cho ba đoạn thẳng AB, BC, CD sao cho . Chứng minh rằng có mặt cầu đi qua bốn điểm A, B, C, D. Tính bán kính mặt cầu đó
- Bài học cùng chủ đề:
- Bài 2 trang 45 SGK Hình học 12 Nâng cao
- Bài 3 trang 45 SGK Hình học 12 Nâng cao
- Bài 4 trang 45 SGK Hình học 12 Nâng cao
- Ngữ pháp tiếng anh hay nhất
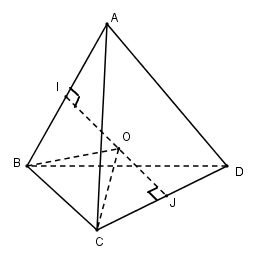
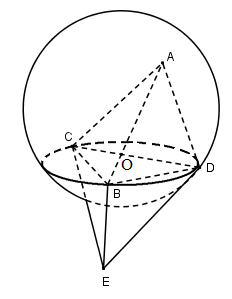
Bài 1. Trong không gian cho ba đoạn thẳng \(AB, BC, CD\) sao cho \(AB \bot BC\,\,,\,\,BC \bot CD\,\,,\,\,CD \bot AB\) . Chứng minh rằng có mặt cầu đi qua bốn điểm \(A, B, C, D\). Tính bán kính mặt cầu đó nếu \(AB = a\,\,,\,\,BC = b\,\,,\,\,CD = c\) .
Giải

Vì \(AB \bot BC\) và \(AB \bot CD\) nên \(AB \bot \left( {BCD} \right)\). Suy ra \(AB \bot BD\)
Vì \(CD \bot BC\) và \(CD \bot AB\) nên \(CD \bot \left( {ABC} \right) \Rightarrow CD \bot AC\)
Gọi \(I\) là trung điểm \(AD\), ta có \(IB = IA = ID = IC\) nên các điểm \(A, B, C, D\) cùng nằm trên mặt cầu đường kính \(AD\).
Mặt khác ta có: \(A{D^2} = A{B^2} + B{D^2} = A{B^2} + B{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\)
Do đó bán kính mặt cầu là \(R = {1 \over 2}AD = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học