Giải bài 19 trang 28 SGK Hình học 12 Nâng cao
Chia sẻ trang này
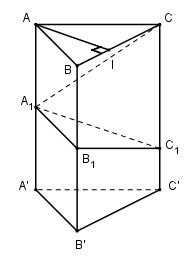
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AC = b. . Đường thẳng BC’ tạo với mp(AA’C’C) một góc . a) Tính độ dài đoạn thẳng AC. b) Tính thể tích khối lăng trụ đã cho.
- Bài học cùng chủ đề:
- Bài 20 trang 28 SGK Hình học 12 Nâng cao
- Bài 21 trang 28 SGK Hình học 12 Nâng cao
- Bài 22 trang 28 SGK Hình học 12 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Bài 19. Cho khối lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác \(ABC\) vuông tại \(A, AC = b\). \(\widehat {ACB} = {60^0}\). Đường thẳng \(BC’\) tạo với mp \((AA’C’C)\) một góc \({30^0}\).
a) Tính độ dài đoạn thẳng \(AC\).
b) Tính thể tích khối lăng trụ đã cho.
Giải
a) Ta có: \(BA \bot AC\) và \(BA \bot AA'\) nên \(BA \bot \left( {ACC'A'} \right)\)
Vậy \(AC’\) là hình chiếu của \(BC’\) trên mp \((ACC’A’)\) nên \(\widehat {AC'B} = {30^0}\)
Trong tam giác vuông \(BAC’\), ta có: \(\cot {30^0} = {{AC'} \over {AB}} \Rightarrow AC' = AB.cot{30^0} = AC.\tan {60^0}.\cot {30^0} = b\sqrt 3 .\sqrt 3 = 3b\)
b) Trong tam giác vuông \(ACC’\), ta có: \(CC{'^2} = AC{'^2} - A{C^2} = 9{b^2} - {b^2} = 8{b^2} \Rightarrow CC' = 2\sqrt 2 b\)
Diện tích là: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}b\sqrt 3 .b = {{{b^2}\sqrt 3 } \over 2}\)
Thể tích khối lăng trụ \(V = S.h = {{{b^2}\sqrt 3 } \over 2}.2\sqrt 2 b = {b^3}\sqrt 6 \)
loigaihay.com
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học
