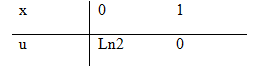
Giải bài 16 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
Chia sẻ trang này
Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu 25 m/s. gia tốc trọng trường là .
Bài 16. Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu 25 m/s. gia tốc trọng trường là \(9,8\,m/{s^2}\).
a) Sau bao lâu viên đạn đạt tới vận tốc cao nhất.
b) Tính quãng đường viên đạn đi được tính từ lúc bắn lên cho đến khi rơi xuống đất.
Giải
a) Gọi v(t) là vận tốc của viên đạn. ta có
Suy ra \(v\left( t \right) = - 9,8t + C.\) vì \(v(0)=25\) nên suy ra \(C=25\)
Vậy \(v\left( t \right) = - 9,8t + 25.\)
Gọi T là thời điểm viên đạn đạt tốc độ cao nhất. tại đó vận tốc viên đạn có vận tốc bằng 0. Vậy \(v(T)=0\) suy ra \(T = {{25} \over {9,8}} \approx 2,55\,\) (giây).
b) Quãng đường viên đi được cho tới thời điểm \(T=2,55\) (giây) là:
\(S = \int\limits_0^T {\left( { - 9,8t + 25} \right)dt} = - 9,8{{{T^2}} \over 2} + 25T \approx 31,89\,\left( m \right)\)
Vậy quãng đường viên đạn đi được cho đến khi rơi là xuống đất là \(2S = 63,78\left( m \right).\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học
