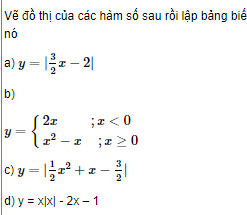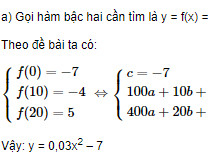Giải bài 38 trang 61 SGK Đại số 10 nâng cao

Chia sẻ trang này

Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).

Ngữ pháp tiếng anh hay nhất

(Bài toán về cổng Ac-xơ (Arch))

Khi du lịch đến thành phố Xanh lu-i (Mĩ) bạn sẽ thấy một cái cổng lớn hình parabol hướng bề lõm về phía dưới. Đó là cổng Ac-xơ. Giả sử lập một hệ tọa độ Oxy sao cho một chân cổng đi qua gốc O như hình vẽ dưới đây (x, y tính bằng mét), chân kia của cổng ở vị trí (162; 0). Biết một điểm M trên cổng có tọa độ là (10; 43).

a) Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).

b) Tính chiều cao của công (Tính từ điểm cao nhất trên cổng xuống mặt đất, tính chính xác đến hàng đơn vị).

Đáp án

a) Giả sử hàm số bậc hai có đồ thị chứa cung parabol trên là:

\(f(x) = ax^2 + bx + c\)

Theo đề bài, ta có:

\(\left\{ \matrix{
f(0) = 0 \hfill \cr
f(10) = 43 \hfill \cr
f(162) = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
c = 0 \hfill \cr
100a + 10b + c = 43 \hfill \cr
162{a^2} + 162b + c = 0 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{
c = 0 \hfill \cr
100a + 10b = 43 \hfill \cr
162a + b = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - {{43} \over {1520}} \hfill \cr
b = {{3483} \over {760}} \hfill \cr} \right.\)

Vậy: \(f(x) = - {{43} \over {1520}}{x^2} + {{3483} \over {760}}x\)

b) Chiều cao của cổng bằng tung độ của đỉnh parabol, tức là:

\({y_0} = f( - {b \over {2a}}) = f(81) \approx 186\,(m)\)

Trên đây là bài học "Giải bài 38 trang 61 SGK Đại số 10 nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 10" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 10 của dayhoctot.com.