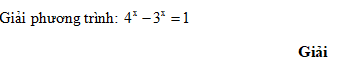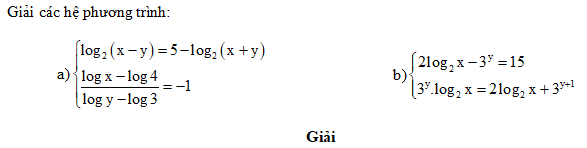Giải bài 86 trang 130 SGK giải tích 12 nâng cao
Tính:
- Bài học cùng chủ đề:
- Bài 87 trang 130 SGK giải tích 12 nâng cao
- Bài 88 trang 130 SGK giải tích 12 nâng cao
- Bài 89 trang 131 SGK giải tích 12 nâng cao
- Ngữ pháp tiếng anh hay nhất
Bài 86. Tính:
\(a)\,A = {9^{2{{\log }_3}4 + 4{{\log }_{81}}2}}\)
\(b)\,B = {\log _a}\left( {{{{a^2}.\root 3 \of a .\root 5 \of {{a^4}} } \over {\root 4 \of a }}} \right)\)
\(c)\,\,C = {\log _5}{\log _5}\root 5 \of {\root 5 \of {\root 5 \of {....\root 5 \of 5 } } } \)
Giải
a) Áp dụng \({\log _{{a^\alpha }}}{b^\beta } = {\beta \over \alpha }{\log _a}b\) (với \(a > 0, b>0\) và \(a \ne 1\)) và \({a^{{{\log }_a}b}} = b\)
Ta có:
\(\eqalign{
& 2{\log _3}4 + 4{\log _{81}}2 = {4 \over 2}{\log _3}4 + 2{\log _9}2 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\log _9}{4^4} + {\log _9}{2^2} = {\log _9}{2^{10}} \cr} \)
Do đó \(A = {9^{{{\log }_9}{2^{10}}}} = {2^{10}} = 1024\)
b) Ta có \({{{a^2}.\root 3 \of a .\root 5 \of {{a^4}} } \over {\root 4 \of a }} = {a^{2 + {1 \over 3} + {4 \over 5} - {1 \over 4}}} = {a^{{{173} \over {60}}}}\)
Do đó: \(B = {\log _a}{a^{{{173} \over {60}}}} = {{173} \over {60}}\)
c) Ta có \(\root 5 \of {\root 5 \of {\root 5 \of {....\root 5 \of 5 } } } = {5^{{{\left( {{1 \over 5}} \right)}^n}}} \Rightarrow {\log _5}\root 5 \of {\root 5 \of {\root 5 \of {....\root 5 \of 5 } } } = {\left( {{1 \over 5}} \right)^n} = {5^{ - n}}\)
\( \Rightarrow C = - n\)
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học