Giải câu 3 trang 99 SGK Hình học 10
Chia sẻ trang này
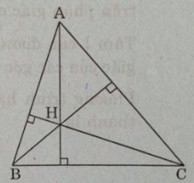
Cho tam giác đều ABC cạnh a
- Bài học cùng chủ đề:
- Câu 4 trang 99 SGK Hình học 10
- Câu 5 trang 99 SGK Hình học 10
- Câu 6 trang 99 SGK Hình học 10
- Ngữ pháp tiếng anh hay nhất
Bài 3. Cho tam giác đều \(ABC\) cạnh \(a\)
a) Cho \(M\) là một điểm trên đường tròn ngoại tiếp tam giác \(ABC\). Tính \(MA^2+ MB^2+ MC^2\) theo \(a\)
b) Cho đường thẳng \(a\) tùy ý, tìm điểm \(N\) trên đường thẳng \(d\) sao cho \(NA^2+ NB^2 + NC^2\) nhỏ nhất
Trả lời:
a) Ta có:
\(\eqalign{
& \overrightarrow {MA} = \overrightarrow {OA} - \overrightarrow {OM} \cr
& {\overrightarrow {MA} ^2} = {(\overrightarrow {OA} - \overrightarrow {OM} )^2} = {\overrightarrow {OA} ^2} + {\overrightarrow {OM} ^2} - 2\overrightarrow {OA} .\overrightarrow {OM} \cr
& \Rightarrow {\overrightarrow {MA} ^2} = 2{R^2} - 2\overrightarrow {OA} .\overrightarrow {OM} (1) \cr} \)
Tương tự ta có:
\(\eqalign{
& M{B^2} = {\overrightarrow {MB} ^2} = 2{R^2} - 2\overrightarrow {OB} .\overrightarrow {OM} (2) \cr
& M{C^2} = {\overrightarrow {MC} ^2} = 2{R^2} - 2\overrightarrow {OC.} \overrightarrow {OM} (3) \cr} \)
Từ (1), (2) và (3) suy ra:
\(M{A^2} + M{B^2} + M{C^2} = 6{R^2} - 2\overrightarrow {OM} (\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\)
Tam giác \(ABC\) là tam giác đều nội tiếp đường tròn tâm \(O\) nên \(O\) cũng là trọng tâm của tam giác \(ABC\), cho ta \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0\)
Vậy \(M{A^2} + M{B^2} + M{C^2} = 6{R^2} \)
Vì đường tròn ngoại tiếp tam giác đều cạnh \(a\) nên ta có:
\(a = R\sqrt3 ⇒ 6R^2= 2(R\sqrt3)^2\)
Vậy \(M{A^2} + M{B^2} + M{C^2} = 2a^2\)
b) Gọi \(G\) là trọng tâm của tam giác ta có:
\(\eqalign{
& \overrightarrow {NA} = \overrightarrow {NG} + \overrightarrow {GA} \cr
& \Rightarrow {\overrightarrow {NA} ^2} = {\overrightarrow {GA} ^2} + 2\overrightarrow {NG} .\overrightarrow {GA} + {\overrightarrow {GA} ^2} \cr} \)
Tương tự ta có:
\(\eqalign{
& {\overrightarrow {NB} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GB} + {\overrightarrow {GB} ^2} \cr
& {\overrightarrow {NC} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GC} + {\overrightarrow {GC} ^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = 3N{G^2} + 2\overrightarrow {NG} (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} ) + G{A^2} + G{B^2} + G{C^2} \cr} \)
Vì \(G\) là trọng tâm của tam giác
⇒ \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\(\eqalign{
& {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} = 3G{A^2} = 3.{({2 \over 3}.{{a\sqrt 3 } \over 2})^2} = {a^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = {a^2} + 3N{G^2} \cr} \)
\(a^2\) là số không đổi nên tổng \(N{A^2} + N{B^2} + N{C^2}\) nhỏ nhất khi \(NG\) đạt giá trị nhỏ nhất. Vì \(NG\) là khoảng cách từ \(G\) đến điểm \(N\) thuộc đường thẳng \(d\) nên \(NG\) nhỏ nhất khi \(NG⊥d\) hay \(N\) là hình chiếu của trọng tâm \(G\) trên đường thẳng \(d\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
