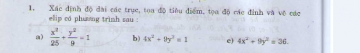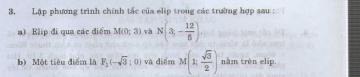Giải bài 8 trang 81 sgk hình học 10
8. Tìm khoảng cách từ điểm đến đường thẳng
Bài 8. Tìm khoảng cách từ điểm đến đường thẳng trong các trường hợp sau:
a) \(A(3; 5)\) \(∆ : 4x + 3y + 1 = 0\);
b) \(B(1; -2)\) \( d: 3x - 4y - 26 = 0\);
c) \(C(1; 2)\) \( m: 3x + 4y - 11 = 0\);
Giải
Áp dụng công thức:
\( d(M_0,∆) = \frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}\)
a) \( d(M_0,∆) =\frac{|4.3+3.5+1|}{\sqrt{4^{2}+3^{2}}}= \frac{28}{5}\)
b) \( d(B,d) =\frac{|3.1-4.(-2)-26|}{\sqrt{3^{2}+(-4)^{2}}} = \frac{-15}{5} = \frac{15}{5} = 3\)
c) Ta có: \(3.1+4.2-11=0\) do đó điểm \(C\) nằm trên đường thẳng \(m\)
\( d(C,m) =0\)
Trên đây là bài học "Giải bài 8 trang 81 sgk hình học 10" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 10" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 10 của dayhoctot.com.
Các bài học liên quan
3. Lập phương trình đường tròn đi qua ba điểm
4. Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm M(2 ; 1)
Lập phương trình của đường tròn tiếp xúc với các trục tọa độ ...
6. Cho đường tròn (C) có phương trình:
1. Xác đinh độ dài các trục, tọa độ tiêu điểm , tọa độ các đỉnh và vẽ các elip có phương trình sau:
2. Lập phương trình chính tắc của elip,
3. Lập phương trình chính tắc của elip trong các trường hợp sau:
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 10