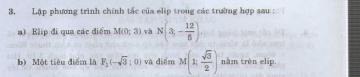Giải bài 4 trang 83 sgk hình học 10
Chia sẻ trang này
4. Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm M(2 ; 1)
- Bài học cùng chủ đề:
- Bài 5 trang 83 sgk hình học 10
- Bài 6 trang 84 sgk hình học 10
- Lý thuyết phương trình đường tròn
- Ngữ pháp tiếng anh hay nhất
Bài 4. Lập phương trình đường tròn tiếp xúc với hai trục tọa độ \(Ox, Oy\) và đi qua điểm \(M(2 ; 1)\)
Giải
Đường tròn tiếp xúc với hai trục tọa độ nên tâm \(I\) của nó phải cách đều hai trục tọa độ. Đường tròn này lại đi qua điểm \(M(2 ; 1)\), mà điểm \(M\) này lại là góc phần tư thứ nhất nên tọa độ của tâm \(I\) phải là số dương.
\(x_I=y_I>0\)
gọi \(x_I=y_I= a\). Như vậy phương trình đường tròn cần tìm là :
\({\left( {2{\rm{ }} - {\rm{ }}a} \right)^2} + {\left( {1{\rm{ }}-{\rm{ }}a} \right)^2} = {a^2}{\rm{ }}\)
\({a^2} - 6a + 5 = 0 \Leftrightarrow \left[ \matrix{
a = 1 \hfill \cr
a = 5 \hfill \cr} \right.\)
Từ đây ta được hai đường tròn thỏa mãn điều kiện
+) Với \(a = 1\) \( \Rightarrow {\left( {x{\rm{ }} - {\rm{ }}1{\rm{ }}} \right)^2} + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}{\rm{ }} = {\rm{ }}1({C_1})\)
+) Với \(a = 5\) \(\Rightarrow {\left( {x - 5{\rm{ }}} \right)^2} + {\rm{ }}{\left( {y - 5} \right)^2}{\rm{ }} = {\rm{ 25}}({C_2})\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
