Giải bài 4 sgk trang 40 hình học 10
Chia sẻ trang này
Chứng minh rằng
- Bài học cùng chủ đề:
- Bài 5 sgk trang 40 hình học 10
- Bài 6 sgk trang 40 hình học 10
- Lý thuyết giá trị lượng giác của một góc bất kỳ từ 0 độ đến 180 độ
- Ngữ pháp tiếng anh hay nhất
Bài 4. Chứng minh rằng với mọi góc \(α (0^0≤ α ≤ 180^0)\) ta đều có \(si{n^2}\alpha + {\cos ^2}\alpha = 1\)
Giải
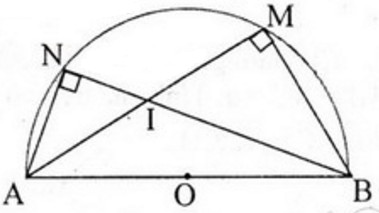
Từ \(M\) kẻ \(MP ⊥ Ox\), \(MQ ⊥ Oy\)
Xét tam giác vuông \(AMP\) có:
\(sin\alpha = {{MP} \over {OM}};\cos \alpha = {{OP} \over {OM}} \)
\(\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = {{M{P^2} + O{P^2}} \over {O{M^2}}} = {{O{M^2}} \over {O{M^2}}} = 1\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
