Giải bài 2 sgk trang 40 hình học 10
Chia sẻ trang này
Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK.
- Bài học cùng chủ đề:
- Bài 3 sgk trang 40 hình học 10
- Bài 4 sgk trang 40 hình học 10
- Bài 5 sgk trang 40 hình học 10
- Ngữ pháp tiếng anh hay nhất
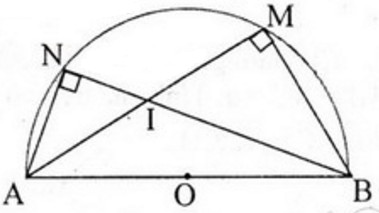
Bài 2. Cho \(AOB\) là tam giác cân tại \(O\) có \(OA = a\) và có các đường cao \(OH\) và \(AK\). Giả sử \(\widehat {AOH} = \alpha \). Tính \(AK\) và \(OK\) theo \(a\) và \(α\).
Giải
Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\alpha \)
Tam giác \(OKA\) vuông tại \(K\) nên ta có:
\(AK = OA.\sin \widehat {AOK} \Rightarrow AK = a.\sin 2\alpha \)
\(OK = OA.cos\widehat {AOK} \Rightarrow OK = a.cos2\alpha \)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
