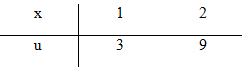Giải bài 45 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Xác định số b dương để tích phân có giá trị lớn nhất.
- Bài học cùng chủ đề:
- Bài 46 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
- Bài 47 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
- Bài 48 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Bài 45. Xác định số b dương để tích phân \(\int\limits_0^b {\left( {x - {x^2}} \right)dx} \) có giá trị lớn nhất.
Giải
Ta có \(\int\limits_0^b {\left( {x - {x^2}} \right)} dx = \left. {\left( {{{{x^2}} \over 2} - {{{x^3}} \over 3}} \right)} \right|_0^b = {{{b^2}} \over 2} - {{{b^3}} \over 3}\)
Xét hàm số \(I\left( b \right) = {{{b^2}} \over 2} - {{{b^3}} \over 3}\) với \(b>0\)
ta có
\(\eqalign{
& I'\left( b \right) = b - {b^2} \cr
& I'\left( b \right) = 0 \Leftrightarrow b = 0;b = 1 \cr} \)
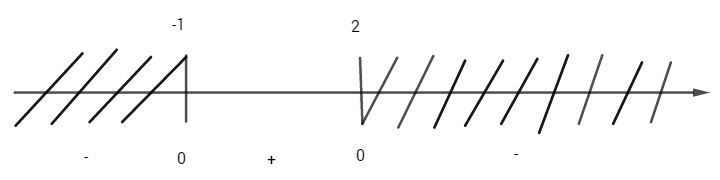
Bảng biến thiên

\( I(b)\) đạt giá trị lớn nhất bằng \({1\over 6}\) khi \(b=1\)
- Chương i. ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Chương ii. hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Chương iii. nguyên hàm, tích phân và ứng dụng
- Chương iv. số phức
- Ôn tập cuối năm đại số và giải tích
- Chương i. khối đa diện và thể tích của chúng
- Chương ii. mặt cầu, mặt trụ, mặt nón
- Chương iii. phương pháp tọa độ trong không gian
- Ôn tập cuối năm hình học