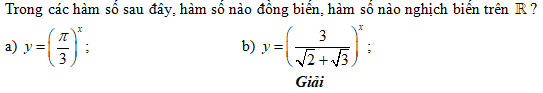
Giải bài 46 trang 97 SGK Đại số và Giải tích 12 Nâng cao

Chia sẻ trang này

Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu239 là 24360 năm (tức là một lượng Pu239 sau 24360 năm phân hủy chỉ còn lại một nửa). Sự phân hủy được tính theo công thức , trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hàng năm (r < 0), t là thời gian phân hủy, S là lượng còn lại sau thời gian phân hủy t. Hỏi 10 gam Pu239 sau bao nhiêu năm phân hủy sẽ còn 1 gam?

Ngữ pháp tiếng anh hay nhất

Bài 46. Cho biết chu kì bán hủy của chất phóng xạ Plutôni \(P{u^{239}}\) là 24360 năm (tức là một lượng \(P{u^{239}}\) sau 24360 năm phân hủy chỉ còn lại một nửa). Sự phân hủy được tính theo công thức \(S = A.{e^{rt}}\), trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hàng năm (r < 0), t là thời gian phân hủy, S là lượng còn lại sau thời gian phân hủy t. Hỏi 10 gam \(P{u^{239}}\) sau bao nhiêu năm phân hủy sẽ còn 1 gam?

Giải

Trước tiên, ta tìm tỉ lệ phân hủy hàng năm của \(P{u^{239}}\).
\(P{u^{239}}\) có chu kì bán hủy là 24360 năm , do đó ta có:

\(5 = 10.{e^{r.24360}}\).
Suy ra:

\(r = {{\ln 5 - \ln 10} \over {24360}} \approx - 2,{84543.10^{ - 5}} \approx - 0,000028\)

Vậy sự phân hủy của \(P{u^{239}}\) được tính theo công thức: \(S = A.{e^{ - 0,000028t}}\)
Trong đó S và A tính bằng gam, t tính bằng năm.
Theo bài ra, ta có: \(1 = 10.{e^{ - 0,000028t}}\)
Suy ra: \(t = {{ - \ln 10} \over { - 0,000028}} \approx 82235\) (năm).
Vậy sau khoảng 82235 năm thì 10 gam chất \(P{u^{239}}\) sẽ phân hủy còn 1 gam.

Trên đây là bài học "Giải bài 46 trang 97 SGK Đại số và Giải tích 12 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 2 lớp 12" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 12 của dayhoctot.com.