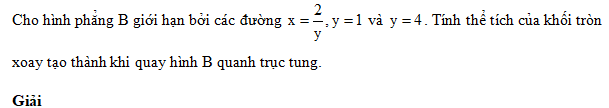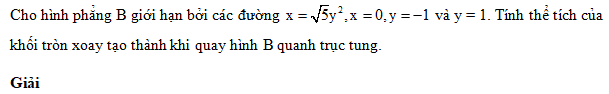
Giải bài 27 Trang 167 SGK Đại số và Giải tích 12 Nâng cao

Bài trước
Bài sau  

Tính diện tích hình phẳng giới hạn bởi:

 Bài 27. Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi ;\)
b) Đồ thị hai hàm số \(y = \sqrt x \) và \(y = \root 3 \of x ;\)
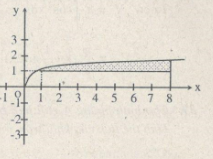
c) Đồ thị hàm số \(y = 2{x^2}\) và \(y = {x^4} - 2{x^2}\) trong miền \(x \ge 0.\)

Giải

a) \(S = \int\limits_0^\pi  {{{\cos }^2}xdx = {1 \over 2}} \int\limits_0^\pi  {\left( {1 + \cos 2x} \right)} dx = \left. {{1 \over 2}\left( {x + {1 \over 2}\sin 2x} \right)} \right|_0^\pi  = {\pi  \over 2}\)
b) Phương trình hoành độ giao điểm của hai đồ thị là \(\sqrt x  = \root 3 \of x  \Leftrightarrow x = 0;x = 1\)
Trên đoạn \(\left[ {0;1} \right]\) thì \(\root 3 \of x  \ge \sqrt x \) nên:

\(S = \int\limits_0^1 {\left( {\root 3 \of x  - \sqrt x } \right)} dx = \int\limits_0^1 {\left( {{x^{{1 \over 3}}} - {x^{{1 \over 2}}}} \right)} dx = \left. {\left( {{3 \over 4}{x^{{4 \over 3}}} - {2 \over 3}{x^{{3 \over 2}}}} \right)} \right|_0^1 = {3 \over 4} - {2 \over 3} = {1 \over {12}}\)

c)Trong miền \(x \ge 0\) hoành độ giao điểm của hai đồ thị là nghiệm phương trình:

\(\left\{ \matrix{
x \ge 0 \hfill \cr
{x^4} - 2{x^2} = 2{x^2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge 0 \hfill \cr
{x^2}\left( {{x^2} - 4} \right) = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right.\)

Ta có: \(S = \int\limits_0^2 {\left| {{x^4} - 2{x^2} - 2{x^2}} \right|} dx = \int\limits_0^2 {\left| {{x^2}\left( {{x^2} - 4} \right)} \right|} dx = \int\limits_0^2 {\left( {4{x^2} - {x^4}} \right)} dx\)

\( = \left. {\left( {4{{{x^3}} \over 3} - {{{x^5}} \over 5}} \right)} \right|_0^2 = {{64} \over {15}}\)

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 12

Bài học nổi bật nhất

Đề thi lớp 12 mới cập nhật