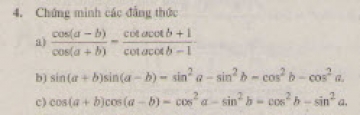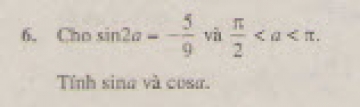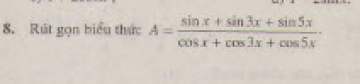Lý thuyết công thức lượng giác
1. Công thức cộng
1. Công thức cộng
\(\cos(a - b) = \cos a\cos b + \sin a\sin b\)
\(\cos(a + b) = \cos a\cos b - \sin a\sin b\)
\(\sin(a - b) = \sin a\cos b - \sin b\cos a\)
\(\sin(a + b) = \sin a\cos b + \sin b\cos a\)
\(\tan(a - b) = \frac{\tan a -\tan b}{1+\tan a\tan b}\)
2. Công thức nhân đôi
\(\sin 2a = 2\sin a\cos a\)
\(cos2a = \cos^2 a – \sin^2 a\)
\(\tan 2a = \frac{2\tan a}{1-\tan^{2}a}\)
Hệ quả: \(\cos 2a = 2\cos^2 a – 1 = 1 – sin^2 a\)
3.Công thức hạ bậc
\(\cos^2a = \frac{1+\cos2a}{2}\); \(sin^2 a = \frac{1-\cos2a}{2}\)
Trên đây là bài học "Lý thuyết công thức lượng giác" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 10" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 10 của dayhoctot.com.
Các bài học liên quan
Bài 4. Chứng minh các đẳng thức
Bài 5. Tính sin2a, cos2a, tan2a, biết:
Bài 6 trang 154 sgk đại số 10 Tính sina và cosa.
Bài 7. Biến đổi thành tích các biểu thức sau
Bài 8. Rút gọn biểu thức A
Hãy nêu định nghĩa của sinα, cosα và giải thích tại sao ta có:
Nêu định nghĩa của tan α, cot α và giải thích vì sao ta có:
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 10