Giải bài 8 trang 17 sgk hình học lớp 10
Chia sẻ trang này
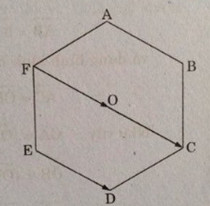
Bài 8. Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
- Bài học cùng chủ đề:
- Bài 9 trang 17 sgk hình học lớp 10
- Lý thuyết tích của vectơ với một số
- Ngữ pháp tiếng anh hay nhất
Bài 8. Cho lục giác \(ABCDEF\). Gọi \(M, N, P, Q, R, S\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DE, EF, FA\). Chứng minh rằng hai tam giác \(MPR\) và \(NQS\) có cùng trọng tâm.
Giải
\(MN\) là đường trung bình của tam giác \(ABC\) nên ta có:
\(\overrightarrow {MN} = {1 \over 2}\overrightarrow {AC} \)
Tương tự ta có:
\(\eqalign{
& \overrightarrow {PQ} = {1 \over 2}\overrightarrow {CE} \cr
& \overrightarrow {RS} = {1 \over 2}\overrightarrow {EA} \cr} \)
\(\eqalign{
& \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = {1 \over 2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right) = {1 \over 2}\overrightarrow {AA} = \overrightarrow 0 \cr
& \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 (1) \cr
& \cr} \)
Gọi \(G\) là trong tâm của tam giác \(MPR\), ta có:
\(\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GR} = \overrightarrow 0 (2)\)
Mặt khác :
\(\eqalign{
& \overrightarrow {MN} = \overrightarrow {MG} + \overrightarrow {GN} \cr
& \overrightarrow {PQ} = \overrightarrow {PG} + \overrightarrow {GQ} \cr
& \overrightarrow {RS} = \overrightarrow {RG} + \overrightarrow {GS} \cr} \)
\(\Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \left( {\overrightarrow {MG} + \overrightarrow {PG} + \overrightarrow {RG} } \right) + \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} (3)\)
Từ (1),(2), (3) suy ra: \(\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GS} = \overrightarrow 0 \)
Vậy \(G\) là trọng tâm của tam giác \(NQS\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
