Giải bài 10 trang 54 sách giáo khoa hình học lớp 11
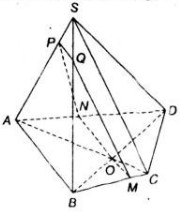
Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
- Bài học cùng chủ đề:
- Lý thuyết Hình biểu diễn của hình không gian
- Lý thuyết Cách xác định một mặt phẳng
- Lý thuyết Khái niệm mở đầu
- Ngữ pháp tiếng anh hay nhất
Bài 10. Cho hình chóp \(S. ABCD\) có \(AB\) và \(CD\) không song song. Gọi \(M\) là một điểm thuộc miền trong của tam giác \(SCD\)
a) Tìm giao điểm \(N\) của đường thẳng \(CD\) và mặt phẳng \((SBM)\)
b) Tìm giao tuyến của hai mặt phẳng \((SBM)\) và \((SAC)\)
c) Tìm giao điểm \(I\) của đường thẳng \(BM\) và mặt phẳng \((SAC)\)
d) Tìm giao điểm \(P\) của \(SC\) và mặt phẳng \((ABM)\), từ đó suy ra giao tuyến của hai mặt phẳng \((SCD)\) và \((ABM)\)
Lời giải:
a) Trong \((SCD)\) kéo dài \(SM\) cắt \(CD\) tại \(N\). Do đó: \(N=CD\cap(SBM)\)
b) \((SBM) ≡ (SBN)\).
Trong \((ABCD)\) gọi \(O=AC\cap BN\)
Do đó: \(SO=(SAC)\cap(SBM)\).
c) Trong \((SBN)\) gọi \(I\) là giao của \(MB\) và \(SO\).
Do đó: \(I=BM\cap (SAC)\)
d) Trong \((ABCD)\) , gọi giao điểm của \(AB\) và \(CD\) là \(K\).
Trong \((SCD)\), gọi \(P= MK\cap SC\)
Do đó: \(P=SC\cap (ABM)\)
Trong \((SDC)\) gọi \(Q=MK\cap SD\)
Từ đó suy ra được giao tuyến của hai mặt phẳng \((SCD)\) và (\(ABM)\) là \(KQ\).