Giải bài 1 trang 59 sách giáo khoa hình học lớp 11
Chia sẻ trang này
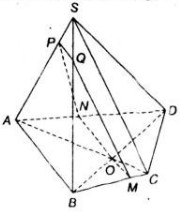
Cho tứ diện ABCD. Gọi P, Q, R, S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD, DA. Chứng minh rằng nếu bốn điểm P, Q, R, S đồng phẳng thì
- Bài học cùng chủ đề:
- Bài 2 trang 59 sách giáo khoa hình học lớp 11
- Bài 3 trang 60 sách giáo khoa hình học lớp 11
- Lý thuyết Vị trí tương đối giữa hai đường thẳng trong mặt phẳng
- Ngữ pháp tiếng anh hay nhất
Bài 1. Cho tứ diện \(ABCD\). Gọi \(P, Q, R, S\) là bốn điểm lần lượt lấy trên bốn cạnh \(AB, BC, CD, DA\). Chứng minh rằng nếu bốn điểm \(P, Q, R, S\) đồng phẳng thì
a) Ba đường thẳng \(PQ, SR, AC\) hoặc song song hoặc đồng quy
b) Ba đường thẳng \(PS, RQ, BD\) hoặc song song hặc đồng quy
Lời giải:
a) Gọi mặt phẳng qua bốn điểm \(P, Q, R, S\) là \((α)\). Ba mặt phẳng \(( α)\), \((ABC)\) và \((ACD)\) đôi một cắt nhau theo các giao tuyến là \(PQ, AC, RS => PQ, AC, RS\) hoặc đôi một song song hoặc đồng quy
b) Chứng minh tương tự ta được ba đường thẳng \(PS, RQ\), và \(BD\) hoặc song song hoặc đồng quy
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
