Giải bài 3 trang 119 sgk Hình học 11
Chia sẻ trang này
Cho hình lập phương ABCD.A'B'C'D'cạnh a....
- Bài học cùng chủ đề:
- Bài 4 trang 119 sgk Hình học 11
- Bài 5 trang 119 sgk Hình học 11
- Bài 6 trang 119 sgk Hình học 11
- Ngữ pháp tiếng anh hay nhất
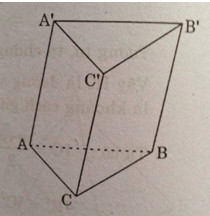
Bài 3. Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Chứng minh rằng các khoảng cách từ các điểm \(B, C, D, A', B', D'\) đến đường chéo \(AC'\) đều bằng nhau. Tính khoảng cách đó.
Giải
(H.3.64)
Gọi \(K\) là hình chiếu của \(B\) trên \(AC'\).
Xét tam giác \(ABC'\) vuông tại \(B\), ta có:
\(\frac{1}{BK^{2}}=\frac{1}{BA^{2}}+\frac{1}{BC^{2}}=\frac{1}{a^{2}}+\frac{1}{(a\sqrt{2})^{2}}=\frac{3}{2a^{2}}\)
\(\Rightarrow BK=\frac{a\sqrt{6}}{3}.\)
Ta có:
\(\Delta ABC' = \Delta C'CA = \Delta ADC' = \Delta AA'C' = \Delta C'B'A = \Delta C'D'A(c.g.c)\)
Do đó khoảng cách từ \(B, C, D, A', B', D'\) tới \(AC'\) đều bằng \( \frac{a\sqrt{6}}{3}\) vì chúng đều là chiều cao của các tam giác vuông bằng nhau.
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
