Giải bài 4 trang 119 sgk Hình học 11
Chia sẻ trang này
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC= b, CC' = c...
- Bài học cùng chủ đề:
- Bài 5 trang 119 sgk Hình học 11
- Bài 6 trang 119 sgk Hình học 11
- Bài 7 trang 120 sgk Hình học 11
- Ngữ pháp tiếng anh hay nhất
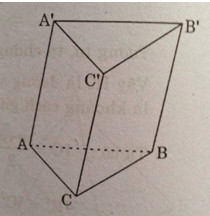
Bài 4. Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a, BC= b, CC' = c\).
a) Tính khoảng cách từ \(B\) đến mặt phẳng \((ACC'A')\).
b) Tính khoảng cách giữa hai đường thẳng \(BB'\) và \(AC'\).
Giải
(H.3.65)
a) Trong \((ABCD)\) kẻ \(BH\) vuông góc với \(AC\) (1)
\(CC'\bot (ABCD)\Rightarrow CC'\bot BH\) (2)
Từ (1) và (2) suy ra \(BH\bot (ACC'A')\).
\(BH\) là đường cao trong tam giác vuông \(ABC\) nên ta có:
\({1 \over {B{H^2}}} = {1 \over {A{B^2}}} + {1 \over {B{C^2}}}\)
\(\Rightarrow BH=\frac{ab}{\sqrt{a^{2}+b^{2}}}.\)
b) \(AC'\subset (ACC'A')\), mà \(BB' // (ACC'A')\) \(\Rightarrow d(BB', AC') = d(B,(ACC'A'))=BH=\frac{ab}{\sqrt{a^{2}+b^{2}}}.\)
(Chú ý: Khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\) bằng khoảng cách giữa \(a\) và \(mp (P)\) chứa \(b\) đồng thời song song với \(a\)).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
