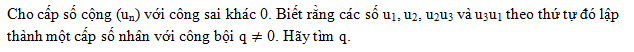
Giải câu 33 trang 121 SGK Đại số và Giải tích 11 Nâng cao

Chia sẻ trang này

Cho cấp số nhân (un)

Bài 33. Cho cấp số nhân (u_n) với công bội \(q ≠ 0\) và \({u_1} \ne 0\). Cho các số nguyên dương m và k, với \(m ≥ k\). Chứng minh rằng \({u_m} = {u_k}.{q^{m - k}}\)

Áp dụng

a. Tìm công bội q của cấp số nhân (u_n) có \({u_4} = 2\) và \({u_7} = - 686\).

b. Hỏi có tồn tại hay không một cấp số nhân (u_n) mà \({u_2} = 5\) và \({u_{22}} = - 2000\) ?

Giải:

Ta có:

\(\eqalign{
& {u_m} = {u_1}.{q^{m - 1}}\,\,\left( 1 \right) \cr
& {u_k} = {u_1}.{q^{k - 1}}\,\,\left( 2 \right) \cr} \)

Lấy (1) chia (2) ta được :

\({{{u_m}} \over {{u_k}}} = {q^{m - k}} \Rightarrow {u_m} = {u_k}.{q^{m - k}}\)

Áp dụng :

a. Ta có:

\({{{u_7}} \over {{u_4}}} = {q^{7 - 4}} \Rightarrow {q^3} = - 343 \Rightarrow q = - 7\)

b. Không tồn tại

\({q^{20}} = {{{u_{22}}} \over {{u_2}}} = {{ - 2000} \over 5} < 0,\) vô lí.

Trên đây là bài học "Giải câu 33 trang 121 SGK Đại số và Giải tích 11 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 11" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 11 của dayhoctot.com.