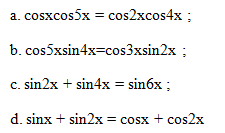Giải câu 24 trang 31 SGK Đại số và Giải tích 11 Nâng cao

Bài trước
Bài sau  

Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất

Bài 24. Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất

như hình 1.23 : điểm \(M\) mô tả cho con tàu, đường thẳng \(∆\) mô tả cho đường xích đạo.

Khoảng cách \(h\) (kilomet) từ \(M\) đến \(∆\) được

tính theo công thức \(h = |d|\), trong đó

\(d = 4000\cos \left[ {{\pi \over {45}}\left( {t - 10} \right)} \right],\)

Với \(t\) (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, \(d > 0\) nếu \(M\) ở phía trên \(∆\), \(d < 0\) nếu \(M\) ở phía dưới \(∆\).

a. Giả thiết rằng con tàu đi vào quỹ đạo ngay từ khi phóng lên tại mũi Ca-na-vơ-ran (tức là ứng với \(t = 0\)). Hãy tính khoảng cách từ điểm \(C\) đến đường thẳng \(∆\), trong đó \(C\) là điểm trên bản đồ biểu diễn cho mũi Ca-na-vơ-ran.

b. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có \(d = 2000\).

c. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có \(d = -1236\).

(Tính chính xác các kết quả đến hàng phần nghìn).

Giải

a. Vì \(t = 0\) nên \(d = 4000\cos \left( { - {{10\pi } \over {45}}} \right) = 4000\cos {{2\pi } \over 9}.\) Do đó :

\(h = |d| ≈ 3064,178 (km)\)

b.

\(\eqalign{& d = 2000 \Leftrightarrow 4000\cos \left[ {{\pi \over {45}}\left( {t - 10} \right)} \right] = 2000\Leftrightarrow \cos \left[ {{\pi \over {45}}\left( {t - 10} \right)} \right] = {1 \over 2} \cr & \Leftrightarrow {\pi \over {45}}\left( {t - 10} \right) = \pm {\pi \over 3} + k2\pi \Leftrightarrow t = 10 \pm 15 + 90k \Leftrightarrow \left[ {\matrix{{t = 25 + 90k} \cr {t = - 5 + 90k} \cr} } \right. \cr} \) 

Chú ý rằng \(t > 0\) ta thấy ngay giá trị nhỏ nhất của \(t\) là \(t = 25\). Vậy \(d = 2000 (km)\) xảy ra lần đầu tiên sau khi phóng con tàu vào quỹ đạo được \(25\) phút.

c.

\(\eqalign{
& d = - 1236 \Leftrightarrow 4000\cos \left[ {{\pi \over {45}}\left( {t - 10} \right)} \right] = - 1236 \Leftrightarrow \cos \left[ {{\pi \over {45}}\left( {t - 10} \right)} \right] = - 0,309 \cr
& \Leftrightarrow {\pi \over {45}}\left( {t - 10} \right) = \pm \alpha + k2\pi \,\left( {\text{ với }\,k \in \mathbb Z\,\text{ và }\,\cos \alpha = - 0,309} \right) \cr
& \Leftrightarrow t = \pm {{45} \over \pi }\alpha + 10 + 90k \cr} \) 

Sử dụng bảng số hoặc máy tính bỏ túi, ta có thể chọn \(α ≈ 1,885\). Khi đó ta có :

\(t ≈ ± 27,000 + 10 + 90k\), tức là \(t ≈ - 17,000 + 90k\) hoặc \(t ≈ 37,000 + 90k\)

Dễ thấy giá trị dương nhỏ nhất của \(t\) là \(37,000\). Vậy \(d = -1236 (km)\) xảy ra lần đầu tiên là \(37,000\) phút sau khi con tàu được phóng vào quỹ đạo. 

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 11

Bài học nổi bật nhất

Đề thi lớp 11 mới cập nhật