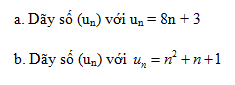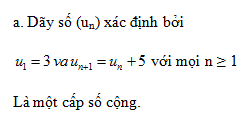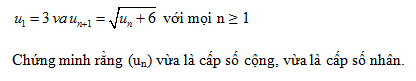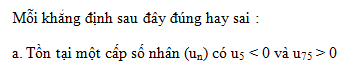
Giải câu 42 trang 122 SGK Đại số và Giải tích 11 Nâng cao

Bài trước
Bài sau  

Hãy tìm ba số hạng đầu tiên

Bài 42. Hãy tìm ba số hạng đầu tiên của một cấp số nhân, biết rằng tổng của chúng bằng \({{148} \over 9}\) và đồng thời các số hạng đó tương ứng là số hạng đầu, số hạng thứ tư và số hạng thứ tám của một cấp số cộng.

Giải:

Kí hiệu u1, u2, u3 lần lượt là số hạng thứ nhất, thứ hai và thứ ba của cấp số nhân nói trong đề bài; gọi q là công bội của cấp số nhân đó.

Gọi d là công sai của cấp số cộng nhận u1, u2 và u3 tương ứng là số hạng thứ nhất, thứ tư và thứ tám.

Ta có: u1 ≠ 0, vì nếu ngược lại thì u2 = u3= 0, và do đó  \({u_1} + {u_2} + {u_3} = 0 \ne {{148} \over 9}.\)

Từ các giả thiết của đề bài ta có :  \({u_2} = {u_1}q = {u_1} + 3d\,\text{ và }\,{u_3} = {u_2}q = {u_2} + 4d\)

Suy ra:

\(\eqalign{
& {u_1}\left( {q - 1} \right) = 3d\,\,\,\,\,\,\,\,\left( 1 \right) \cr
& {u_2}\left( {q - 1} \right) = 4d\,\,\,\,\,\,\,\left( 2 \right) \cr} \)

Xét hai trường hợp sau :

* Trường hợp 1 : q ≠ 1. Khi đó (1) và (2) suy ra d ≠ 0 (do u1≠ 0) và  \(q = {{{u_2}} \over {{u_1}}} = {4 \over 3}\)

Từ đó :

\(\eqalign{
& {{148} \over 9} = {u_1} + {u_2} + {u_3} = {u_1}.{{1 - {q^3}} \over {1 - q}} \cr
& = {u_1}.{{1 - {{\left( {{4 \over 3}} \right)}^3}} \over {1 - {4 \over 3}}} = {u_1}.{{37} \over 9} \Rightarrow {u_1} = 4 \cr
& \Rightarrow {u_2} = {u_1}q = {{16} \over 3} \Rightarrow {u_3} = {u_2}q = {{64} \over 9} \cr} \)

Ta có ba số vừa tìm được ở trên là các số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng có công sai  

\(d = {4 \over 9}.\)

* Trường hợp 2 : q = 1. Khi đó \({u_1} = {u_2} = {u_3}\) . Vì thế  \({{148} \over 9} = 3{u_1}.\)

Suy ra:  \({u_1} = {u_2} = {u_3} = {{148} \over {27}}\)

Hiển nhiên ba số vừa tìm được ở trên là các số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng với công sai d = 0. Vậy có hai bộ ba số cần tìm là :

\({u_1} = 4,{u_2} = {{16} \over 3},{u_3} = {{64} \over 9}\,\text{ và }\,{u_1} = {u_2} = {u_3} = {{148} \over {27}}.\)

  dayhoctot.com

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 11

Bài học nổi bật nhất

Đề thi lớp 11 mới cập nhật