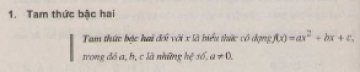Lý thuyết phương trình quy về phương trình bậc nhất, bậc hai
Chia sẻ trang này
Giải và biện luận phương trình dạng ax + b = 0
Lý thuyết phương trình quy về phương trình bậc nhất, bậc hai
Tóm tắt lý thuyết
1. Giải và biện luận phương trình dạng \(ax + b = 0\) (1)
\(a≠ 0\) : (1) có nghiệm duy nhất \(x = \frac{-b}{a}\).
\(a = 0\); \(b ≠ 0\) (1) vô nghiệm.
\(a=0\); \(b = 0\): (1) nghiệm đúng với mọi \(x ∈\mathbb R\).
Ghi chú: Phương trình \(ax + b = 0\) với \(a ≠ 0\) được gọi là phương trình bậc nhất một ẩn \(x\)
2. Phương trình bậc hai một ẩn \(ax^2+ bx + c= 0 (a ≠ 0)\) (2)
\(∆ = b^2-4ac\) được gọi là biệt thức của phương trình (2).
+ \(∆ > 0\) thì (2) có nghiệm phân biệt \(x_{1,2}= \frac{-b \pm \sqrt{\Delta }}{2a}\)
+ \(∆ = 0\) thì (2) có 2 nghiệm kép \(x= -\frac{b}{2a}\)
+ \(∆ < 0\) thì (2) vô nghiệm.
3. Định lí Vi-ét
Nếu phương trình bậc hai \(ax^2+ bx + c= 0\) \((a ≠ 0)\) có hai nghiệm \(x_1,x_2\) thì
\(x_1,x_2= \frac{-b}{a}\), \(x_1.x_2=\frac{c}{a}\).
Đảo lại: Nếu hai số u và v có tổng \(u + v =S\) và tích \(u.v = P\) thì \(u, v\) là các nghiệm của phương trình: \(x^2- Sx + P = 0\).
4. Phương trình chứa dấu giá trị tuyệt đối
Cách giải phương trình chứa ẩn trong dấu giá trị tuyệt đối là đặt các điều kiện xác định để đưa phương trình có dấu giá trị tuyệt đối thành phương trình không dấu giá trị tuyệt đối.
5. Phương trình chứa dấu căn
Đường lối chung để giải phương trình chứa ẩn dưới dấu căn là đặt điều kiện rồi lũy thừa một cách thích hợp hai vế của phương trình để làm mất dấu căn thức.
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
