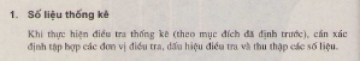
Lý thuyết bất đẳng thức
Chia sẻ trang này
Bất đẳng thức là một mệnh đề có một trong các dạng A > B...
1. Bất đẳng thức là một mệnh đề có một trong các dạng \(A > B, A < B, A B, A B\), trong đó \(A, B\) là các biểu thức chứa các số và các phép toán.
Biểu thức \(A\) được gọi là vế trái, \(B\) là vế phải của bất đẳng thức.
Nếu mệnh đề: \("A < B => C < D"\) là mệnh đề đúng thì ta bảo bất đẳng thức \(C < D\) là hệ quả của bất đẳng thức \(A < B\).
Nếu \("A < B => C < D"\) và \("C < D ⇒ A < B"\) là mệnh đề đúng thì ta nói hai bất đẳng thức \(A < B\) và \(C < D\) tương đương, kí hiệu là \(A < B ⇔ C < D\).
2. Các tính chất của bất đẳng thức.
TC1. ( Tính chất bắc cầu)
\(\left\{ \matrix{
A < B \hfill \cr
B < C \hfill \cr} \right. \Rightarrow A < C\)
TC2. (Quy tắc cộng)
\(A < B ⇔ A + C < B + C\)
TC3. (Quy tắc cộng hai bất đẳng thức dùng chiều)
\(\left\{ \matrix{
A < B \hfill \cr
C < D \hfill \cr} \right. \Rightarrow A + C < B + D\)
TC4. (Quy tắc nhân)
\(\left\{ \matrix{
A < B \hfill \cr
C > 0 \hfill \cr} \right. \Leftrightarrow AC < BC\)
\(\left\{ \matrix{
A < B \hfill \cr
C < 0 \hfill \cr} \right. \Leftrightarrow AC > BC\)
TC5. (Quy tắc nhân hai bất đẳng thức)
\(\left\{ \matrix{
0 < A < B \hfill \cr
0 < C < D \hfill \cr} \right. \Rightarrow AC < B{\rm{D}}\)
TC6. (Quy tắc lũy thừa, khai căn)
Với \(A, B > 0, n ∈\mathbb N^*\) ta có:
\( A < B \Leftrightarrow A^n< B^n\)
\(A < B \Leftrightarrow \root n \of A < \root n \of B \).
3. Bất đẳng thức giữa trung bình cộng và trung bình nhân (Bất đẳng thức Côsi)
Ta gọi \({{a + b} \over 2}\) là trung bình cộng của hai số \(a, b\).
Tổng quát trung bình cộng của n số \({a_1},{a_2},...,{a_n}\) là
\({{{a_1} + {a_2} + ... + {a_n}} \over n}\)
Trung bình nhân của hai số không âm \(a ≥ 0, b ≥ 0\) là \(\sqrt {ab} \)
Trung bình nhân của n số không âm \({a_1} \ge 0,{a_2} \ge 0,...,{a_n} \ge 0\) là
\(\root n \of {{a_1}{a_2}...{a_n}} \)
Định lí: Ta có bất đẳng thức dưới đây, mang tên bất đẳng Cô si:
\(\sqrt {ab} \le {{a + b} \over 2}\) \(∀a, b ≥ 0\).
Dấu \("="\) chỉ xảy ra khi \(a = b\).
Người ta cũng có:
\(\root 3 \of {abc} \le {{a + b + c} \over 3}\) \(∀a, b, c ≥ 0\).
\(\root n \of {{a_1}{a_2}...{a_n}} \le {{{a_1} + {a_2} + ... + {a_n}} \over n}\) \(∀ {a_1},{a_2},...,{a_n} \ge 0\)
Hệ quả 1. Nếu hai số dương có tổng không đổi thì tích của chúng lớn nhất khi hai số bằng nhau.
Hệ quả 2. Nếu hai số dương có tích không đổi thì tổng của chúng nhỏ nhất khi hai số bằng nhau.
4. Bất đẳng thức chứa dấu giá trị tuyệt đối.
Ta có các bất đẳng thức sau:
\(|a + b| ≤ |a| + |b|\) \(∀a, b ∈\mathbb R\)
Dấu \("="\) chỉ xảy ra khi \(ab\)
\(|x| ≤ a \Leftrightarrow - a ≤ x ≤ a\) \(∀a > 0\)
\(|x| ≥ a \Leftrightarrow\left[ {\matrix{{x \ge a} \cr {x \le - a} \cr} } \right.\forall a > 0.\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
