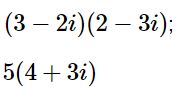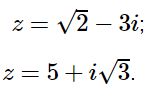
Giải bài 4 trang 134 SGK Giải tích 12
Chia sẻ trang này
Giải bài 4 trang 134 SGK Giải tích 12. Tính |z|
- Bài học cùng chủ đề:
- Bài 5 trang 134 SGK Giải tích 12
- Bài 6 trang 134 SGK Giải tích 12
- Lý thuyết số phức
- Ngữ pháp tiếng anh hay nhất
Đề bài
Tính \(|z|\) với:
a) \(z = -2 + i\sqrt3\); b) \(z = \sqrt2 - 3i\);
c) \(z = -5\); d) \(z = i\sqrt3\).
Phương pháp giải - Xem chi tiết
Cho số phức \(z=x+yi, (x,\, y \in R).\) Khi đó modun của số phức \(z\) được tính bởi công thức: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\)
Lời giải chi tiết
a) \(\left| z \right| = \sqrt{(-2)^{2}+(\sqrt{3})^{2}}=\sqrt{7}\);
b) \(\left| z \right| =\sqrt{(\sqrt{2})^{2}+(-3)^{2}} = \sqrt{11}\);
c) \(\left| z \right| = \sqrt{(-5)^{2}} = 5 \);
d) \(\left| z \right| = \sqrt{(\sqrt{3})^{2}}= \sqrt3\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
