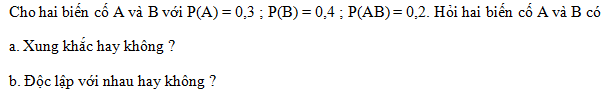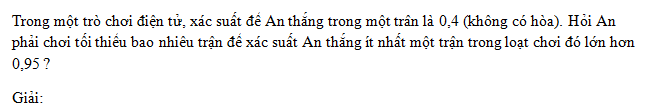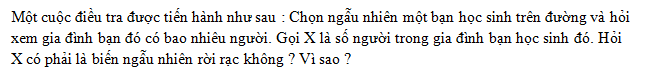Giải câu 34 trang 83 SGK Đại số và Giải tích 11 Nâng cao

Chia sẻ trang này

Bài trước

Bài sau

Gieo ba đồng xu cân đối một cách độc lập. Tính xác suất để:

Bài 34. Gieo ba đồng xu cân đối một cách độc lập. Tính xác suất để :

a. Cả ba đồng xu đều sấp ;

b. Có ít nhất một đồng xu sấp ;

c. Có đúng một đồng xu sấp.

Giải

a. Gọi \(A_i\) là biến cố “Đồng xu thứ i sấp” (\(i = 1,2,3\)), ta có: \(P\left( A \right) = {1 \over 2}.\) Các biến cố \({A_1},{\rm{ }}{A_2},{\rm{ }}{A_3}\) độc lập. Theo quy tắc nhân xác suất, ta có: \(P({A_1}{A_2}{A_3}) = P({A_1})P({A_2})P({A_3})= {1 \over 8}\)

b. Gọi \(H\) là biến cố “Có ít nhất một đồng xu sấp”. Biến cố đối của biến cố \(H\) là \(\overline H \) :”Cả ba đồng xu đều ngửa”. Tương tự như câu a ta có \(P\left( {\overline H } \right) = {1 \over 8}.\) Vậy :

\(P\left( H \right) = 1 - {1 \over 8} = {7 \over 8}\)

c. Gọi \(K\) là biến cố “Có đúng một đồng xu sấp”. Ta có:

\(K = {A_1}\overline {{A_2}} \overline {{A_3}} \cup \overline {{A_1}} {A_2}\overline {{A_3}} \cup \overline {{A_1}} \overline {{A_2}} {A_3}\)

Theo quy tắc cộng xác suất, ta có:

\(P\left( K \right) = P\left( {{A_1}\overline {{A_2}} \overline {{A_3}} } \right) + P\left( {\overline {{A_1}} {A_2}\overline {{A_3}} } \right) + P\left( {\overline {{A_1}} \overline {{A_2}} {A_3}} \right)\)

Theo quy tắc nhân xác suất, ta tìm được :

\(P\left( {{A_1}\overline {{A_2}} \overline {{A_3}} } \right) = P\left( {{A_1}} \right)P\left( {\overline {{A_2}} } \right)P\left( {\overline {{A_3}} } \right) = {1 \over 8}\)

Tương tự \(P\left( {\overline {{A_1}} {A_2}\overline {{A_3}} } \right) = P\left( {\overline {{A_1}} \overline {{A_2}} {A_3}} \right) = {1 \over 8}\).

Từ đó \(P\left( K \right) = {3 \over 8}\)

Trên đây là bài học "Giải câu 34 trang 83 SGK Đại số và Giải tích 11 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 11" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 11 của dayhoctot.com.