Giải bài 4 trang 39 SGK Hình học lớp 12
Chia sẻ trang này
Giải bài 4 trang 39 SGK Hình học lớp 12. Trong không gian cho hai điểm A, B cố định và có độ dài AB = 20 cm,. Gọi d là một đường thẳng thay đổi luôn luôn đi qua A và cách B một khoảng bằng 10 cm
- Bài học cùng chủ đề:
- Bài 5 trang 39 SGK Hình học lớp 12
- Bài 6 trang 39 SGK Hình học lớp 12
- Bài 7 trang 39 SGK Hình học lớp 12
- Ngữ pháp tiếng anh hay nhất
Đề bài
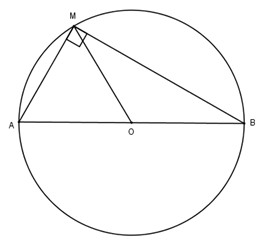
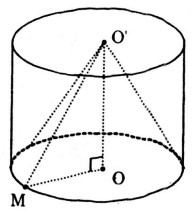
Trong không gian cho hai điểm \(A, B\) cố định và có độ dài \(AB = 20 cm\). Gọi \(d\) là một đường thẳng thay đổi luôn luôn đi qua \(A\) và cách \(B\) một khoảng bằng \(10 cm\). Chứng tỏ rằng đường thẳng \(d\) luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.
Phương pháp giải - Xem chi tiết
Dựa vào định nghĩa hình nón: Trong mặt phẳng \((P)\) cho hai đường thẳng \(d\) và \(\Delta\) cắt nhau tại điểm \(O\) vào tạo thành góc \(\beta\) với \({0^0}<{\beta}<{90^0}\). Khi quay mặt phẳng \((P)\) xung quanh \(\Delta\) thì đường thẳng \(d\) sinh ra một mặt tròn xoay được gọi là mặt nón tròn xoay đỉnh \(O\). Đường thẳng \(\Delta\) gọi là trục, đường thẳng \(d\) gọi là đường sinh và góc \(2\beta\) gọi là góc ở đỉnh của mặt nón đó.
Lời giải chi tiết
Kẻ \(BH \bot d\) ta có \(BH = 10cm\). Gọi \(\alpha = \widehat {BAH}\)
Ta có \(\sin \alpha = {{BH} \over {AB}} = {1 \over 2} \Rightarrow \alpha = {30^0}=const\).
Đường thẳng \(d\) cắt AB tại điểm A và tạo thành góc \(30^0\) nên đường thẳng \(d\) luôn thuộc mặt nón nhận đường thẳng \(AB\) làm trục và có góc ở đỉnh bằng \(2α = 60^0\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
