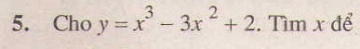Giải bài 5 trang 156 sách giáo khoa Đại số và Giải tích 11
Chia sẻ trang này
5. Viết phương trình tiếp tuyến của đường cong
- Bài học cùng chủ đề:
- Bài 6 trang 156 sách giáo khoa Đại số và Giải tích 11
- Bài 7 trang 157 sách giáo khoa Đại số và Giải tích 11
- Lý thuyết định nghĩa và ý nghĩa của đạo hàm
- Ngữ pháp tiếng anh hay nhất
Bài 5. Viết phương trình tiếp tuyến của đường cong \(y = x^3\):
a) Tại điểm có tọa độ \((-1;-1)\);
b) Tại điểm có hoành độ bằng \(2\);
c) Biết hệ số góc của tiếp tuyến bằng \(3\).
Giải:
Bằng định nghĩa ta tính được \(y' = 3x^2\).
a) \(y' (-1) = 3\). Do đó hệ số góc của tiếp tuyến bằng \(3\). Vậy phương trình tiếp tuyến tại điểm \((-1;-1)\) là \(y - (-1) = 3[x - (-1)]\) hay \(y = 3x+2\).
b) \(y' (2) = 12\). Do đó hệ số góc của tiếp tuyến bằng \(12\). Ngoài ra ta có \(y(2) = 8\). Vậy phương trình tiếp tuyến tại điểm có hoành độ bằng \(2\) là: \( y - 8 = 12(x - 2)\)
hay \(y = 12x -16\).
c) Gọi \(x_0\) là hoành độ tiếp điểm. Ta có:
\(y' (x_0) = 3 \Leftrightarrow 3{x_0}^2= 3\Leftrightarrow {x_0}^2= 1\Leftrightarrow x_0= ±1\).
+) Với \(x_0= 1\) ta có \(y(1) = 1\), phương trình tiếp tuyến là
\( y - 1 = 3(x - 1)\) hay \(y = 3x - 2\).
+) Với \(x_0= -1\) ta có \(y(-1) = -1\), phương trình tiếp tuyến là
\(y - (-1) = 3[x - (-1)]\) hay \(y = 3x + 2\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
