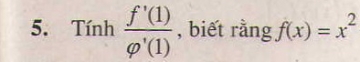
Giải bài 1 trang 162 sách giáo khoa Đại số và Giải tích 11
Chia sẻ trang này
1. Bằng định nghĩa, tìm đạo hàm của các hàm số sau:
- Bài học cùng chủ đề:
- Bài 2 trang 163 sách giáo khoa Đại số và Giải tích 11
- Bài 3 trang 163 sách giáo khoa Đại số và Giải tích 11
- Bài 4 trang 163 sách giáo khoa Đại số và Giải tích 11
- Ngữ pháp tiếng anh hay nhất
Bài 1. Bằng định nghĩa, tìm đạo hàm của các hàm số sau:
a) \(y = 7 + x - x^2\) tại \(x_0 = 1\);
b) \(y = x^3- 2x + 1\) tại \(x_0= 2\).
Giải:
a) Giả sử \(∆x\) là số gia của đối số tại \(x_0= 1\). Ta có:
\(∆y = f(1 + ∆x) - f(1) = 7 + (1 + ∆x) - (1 + ∆x)^2\)
\(- (7 + 1 - 1^2) = -(∆x)^2- ∆x\) ;
\( \frac{\Delta y}{\Delta x} = - ∆x - 1\) ; \(\mathop {\lim}\limits_{\Delta x\rightarrow 0}\)\( \frac{\Delta y}{\Delta x}\) = \( \mathop{\lim}\limits_{\Delta x\rightarrow 0} (- ∆x - 1) = -1\).
Vậy \(f'(1) = -1\).
b) Giả sử \(∆x\) là số gia của số đối tại \(x_0= 2\). Ta có:
\(∆y = f(2 + ∆x) - f(2) = (2 + ∆x)^3-2(2 + ∆x) + 1 \)\(- (2^3- 2.2 + 1) = (∆x)^3+ 6(∆x)^2+ 10∆x\);
\( \frac{\Delta y}{\Delta x} = (∆x)^2+ 6∆x + 10\);
\(\mathop{ \lim}\limits_{\Delta x\rightarrow 0}\)\( \frac{\Delta y}{\Delta x}\) = \( \mathop{\lim}\limits_{\Delta x\rightarrow 0}[(∆x)^2+ 6∆x + 10] = 10\).
Vậy \(f'(2) = 10\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
