Giải câu 32 trang 68 SGK Hình học 11 Nâng cao
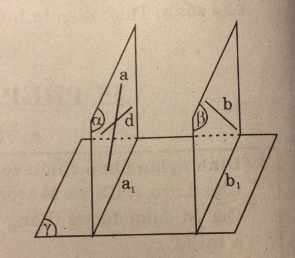
Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b
- Bài học cùng chủ đề:
- Câu 33 trang 68 SGK Hình học 11 Nâng cao
- Câu 34 trang 68 SGK Hình học 11 Nâng cao
- Câu 35 trang 68 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b
Giải:

Giả sử c = mp ( M, a) ∩ mp(M, b). Ta cần chứng minh c cắt cả a và b.
Vì c và a cũng nằm trên một mặt phẳng và không thể trùng nhau ( do c qua M và a không đi qua M) nên hoặc c // a hoặc c cắt a. Cũng vậy, hoặc c // b hoặc c cắt b.
Không thể xảy ra đồng thời c // a; c // b vì a và b chéo nhau. Vậy nếu c song song với a và c phải cắt b, tức là c qua một điểm của mp (Q) và song song với a, suy ra c phải thuộc mp (Q), và do đó M thuộc (Q) (trái giả thiết).
Tương tự, không thể có c song song với b.
Tóm lại c cắt a và b.
Nếu còn có đường thẳng c’ khác c đi qua M, cắt cả a và b thì a và b đồng phẳng. Vô lí.
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học