Giải câu 33 trang 68 SGK Hình học 11 Nâng cao

Bài trước
Bài sau  

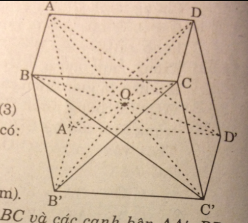
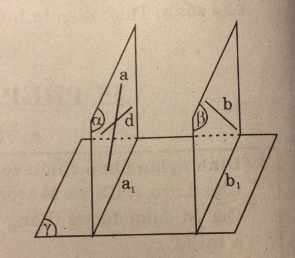
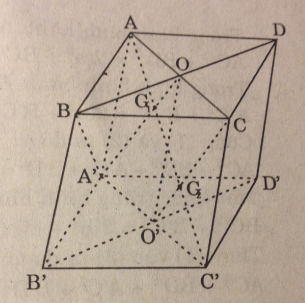
Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành

Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành

Giải

Ta có: \(\left\{ {\matrix{   {a//b}  \cr   {AD//BC } \cr   {a \cap AD=A }  \cr } } \right.\Rightarrow \left( {a,d} \right)//\left( {b,c} \right) \)

Tương tự (a, b) // (c, d).

Vì hai mặt phẳng (a, b) và (c, d) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này

lần lượt theo hai giao tuyến A’B’ và C’D’ song song nhau.

Tương tự A’D’// B’C’.

Vậy A’B’C’D’ là hình bình hành.

Bài trước
In bài này
Bài sau  
Các bài học liên quan

Câu 39 trang 68 SGK Hình học 11 Nâng cao

Cho hình chóp cụt ABC.A’B’C’ có đáy lớn ABC và các cạnh bên AA’, BB’, CC’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và M’, N’, P’ lần lượt là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt
Câu 39 trang 68 SGK Hình học 11 Nâng cao
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 11

Bài học nổi bật nhất

Đề thi lớp 11 mới cập nhật