Giải câu 36 trang 68 SGK Hình học 11 Nâng cao

Chia sẻ trang này

Bài sau

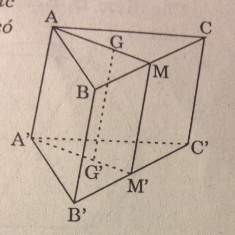
Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.

a. Chứng minh rằng đường thẳng CB’ song song với mp(AHC’)

b. Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (A’BC). Chứng minh rằng d song song với mp(BB’C’C)

c. Xác định thiết diện của hình lăng trụ ABC.A’B’C’khi cắt bởi mp(H , d)

Giải

a) Chứng minh CB' // (AHC’)

Ta tìm trong (AHC’) một đường thẳng song song với CB’, muốn vậy ta tìm giao tuyến của một mặt phẳng chứa CB’ với (AHC’), đó là (A’CB’).

Gọi O là giao điểm AC’ và A’C.

AA’C’C là hình bình hành nên O là trung điểm của A’C.

Do đó HO là đường trung bình của ∆A’B’C

⇒ HO // B’C ⇒ B’C // (AHC’). ( vì HO \(\subset\) (AHC’)).

b) Tìm giao tuyến d của (AB’C’) và (A’BC).

Gọi O’ là giao điểm của AB’ và A’B thì O, O’ là hai điểm chung của hai mặt phẳng (AB’C’) và (A’BC) nên (AB’C’) ∩ (A’BC) = OO’

Vậy d = OO’. Ta có O’ là trung điểm của AB’ ( vì AA’B’B là hình bình hành).

⇒ OO’ là đường trung bình của ∆AB’C’.

⇒ OO’ // B’C' // BC ⇒ OO’ // (BB’C’C) ⇒ d // (BB’C’C)

c) Gọi {K} = HO’ ∩ AB thì HK // AA’

Qua O kẻ ML // AA’ ( M ∈ A’C’, L ∈ AC).

Thiết diện cần tìm là hình bình hành HKLM.

dayhoctot.com

Trên đây là bài học "Giải câu 36 trang 68 SGK Hình học 11 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 11" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 11 của dayhoctot.com.