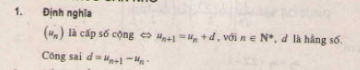Lý thuyết Hoán vị - Chỉnh hợp - Tổ hợp
Chia sẻ trang này
Cho n phần tử khác nhau (n ≥ 1). Mỗi cách sắp thứ tự của
- Bài học cùng chủ đề:
- Lý thuyết nhị thức Niu - Tơn.
- Ngữ pháp tiếng anh hay nhất
Cho \(n\) phần tử khác nhau (\(n ≥ 1\)). Mỗi cách sắp thứ tự của \(n\) phần tử đã cho, mà trong đó mỗi phần tử có mặt đúng một lần, được gọi là một hoán vị của \(n\) phần tử đó.
Định lí
Số các hoán vị của \(n\) phần tử khác nhau đã cho (\(n ≥ 1\)) được kí hiệu là \(P_n\) và bằng:
\(P_n = n(n - 1)(n - 2)...2 . 1 = n!\).
2. Chỉnh hợp:
Định nghĩa:
Cho \(n\) phần tử khác nhau (\(n ≥ 1\)). Mỗi tập con sắp thứ tự gồm \(k\) phần tử khác nhau (\(1 ≤ k ≤ n\)) của tập hợp \(n\) phần tử đã cho được gọi là một chỉnh hợp chập \(k\) của \(n\) phần tử đã cho.
Chú ý:
Mỗi hoán vị của n phần tử khác nhau đã cho chính là một chỉnh hợp chập \(n\) của \(n\) phần tử đó.
Định lí:
Số chỉnh hợp chập \(k\) của \(n\) phần tử khác nhau đã cho được kí hiệu là \(A_n^k\) và bằng
\(A_n^k = n(n – 1)…(n – k + 1) =\frac{n!}{(n - k)!'} (1 ≤ k ≤ n)\),
Với quy ước \(0! = 1\).
3. Tổ hợp:
Định nghĩa:
Cho \(n\) phần tử khác nhau (\(n ≥ 1\)). Mỗi tập con gồm \(k\) phần tử khác nhau (không phân biệt thứ tự) của tập hợp \(n\) phần tử đã cho (\(0 ≤ k ≤ n\)) được gọi là một tổ hợp chập \(k\) của \(n\) phần tử đã cho (với quy ước tổ hợp chập \(0\) của n phần tử bất kỳ là tập rỗng).
Định lí:
Số các tổ hợp chập \(k\) của \(n\) phần tử khác nhau đã cho được kí hiệu là \(C_n^k\) và bằng
\(C_n^k = \frac{n!}{k! (n - k)!}\) = \(\frac{A^{k_{n}}}{k!}\), (\(0 ≤ k ≤ n\)).
Định lí:
Với mọi \(n ≥ 1; 0 ≤ k ≤ n\), ta có:
a) \(C_n^k = C_n^{n-k}\)
b) \(C_n^k + C_n^{k+1}\) = \(C_{n+1}^{k+1}\) ( công thức Pascal).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
