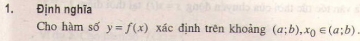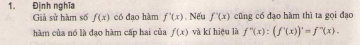Lý thuyết cấp số cộng
Chia sẻ trang này
1. Định nghĩa
1. Định nghĩa
\(U_n\) là cấp số cộng \(u_{n+1}=u_n+ d\) với \(n\in {\mathbb N}^*\), \(d\) là hằng số.
Công sai \(d = u_{n+1}-u_n\)
2. Số hạng tổng quát
\(u_n= u_1+ (n – 1)d, (n ≥ 2)\).
\(d = \frac{u_{n}-u_{1}}{n-1}\).
3. Tính chất
\( u_{k}=\frac{u_{k-1}+u_{k+1}}{2}\) với \(k ≥ 2\) hay \(u_{k+1}+u_{k-1}= 2u_k\)
4. Tổng \(n\) số hạng đầu
\(S_n= \frac{n(u_{1}+u_{n})}{2}\), với \(n\in {\mathbb N}^*\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
