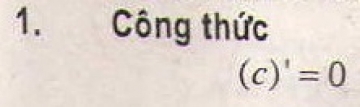
Lý thuyết cấp số nhân
Chia sẻ trang này
1. Định nghĩa un là cấp số nhân un+1 = un.q, với n ε N*
1. Định nghĩa
\(u_n\) là cấp số nhân \(\Leftrightarrow u_{n+1}= u_n.q\), với \(n\in {\mathbb N}^*\)
Công bội \(q = {{{u_{n + 1}}} \over {{u_n}}}\)
2. Số hạng tổng quát: \({u_n} = {u_1}.{q^{n - 1}} ,(n ≥ 2)\)
3. Tính chất: \(u_k^2 = {u_{k - 1}}.{u_{k + 1}}\) hay \(|{u_k}| = {u_{k - 1}}.{u_{k + 1}}\), \(k ≥ 2\)
4. Tổng n số hạng đầu \({S_n} = {{{u_1}({q^n} - 1)} \over {q - 1}}\), \((q ≠ 1)\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
