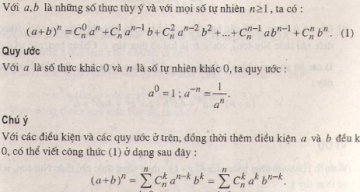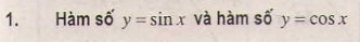
Giải câu 4 trang 126 SGK Hình học 11
Chia sẻ trang này
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có E, F, M và N lần lượt là trung điểm của AC, BD, AC’ và BD’. Chứng minh MN = EF.
- Bài học cùng chủ đề:
- Câu 5 trang 126 SGK Hình học 11
- Câu 6 trang 126 SGK Hình học 11
- Câu 7 trang 126 SGK Hình học 11
- Ngữ pháp tiếng anh hay nhất
Bài 4. Cho hình lăng trụ tứ giác \(ABCD.A’B’C’D’\) có \(E, F, M\) và \(N\) lần lượt là trung điểm của \(AC, BD, AC’\) và \(BD’\). Chứng minh \(MN = EF\).
Giải
Vì \(M\) là trung điểm của \(A’C\) và \(E\) là trung điểm của \(AC\) nên
\(\overrightarrow {EM} = {1 \over 2}\overrightarrow {AA'} (1)\)
Tương tự ta có: \(\overrightarrow {FN} = {1 \over 2}\overrightarrow {BB'} (2)\)
Ta lại có: \(\overrightarrow {AA'} = \overrightarrow {BB'} (3)\)
Từ (1), (2), (3) ⇒ \(\overrightarrow {EM} = \overrightarrow {FN}\) hay tứ giác \(EFNM\) là hình bình hành, do đó \(MN = EF\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
