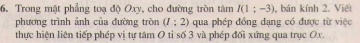Giải bài 4 trang 34 sách giáo khoa hình học lớp 11
Chia sẻ trang này
Cho vectơ v, đường thẳng d vuông góc với giá của vectơ v. Gọi d' là ảnh của d qua phép tịnh tiến theo vectơ.
- Bài học cùng chủ đề:
- Bài 1 trang 35 sách giáo khoa hình học lớp 11
- Bài 2 trang 35 sách giáo khoa hình học lớp 11
- Bài 3 trang 35 sách giáo khoa hình học lớp 11
- Ngữ pháp tiếng anh hay nhất
Bài 4. Cho vectơ \(v\), đường thẳng \(d\) vuông góc với giá của vectơ \(v\). Gọi \(d'\) là ảnh của \(d\) qua phép tịnh tiến theo vectơ \( \frac{1}{2}\) \( \overrightarrow{v}\). Chứng minh rằng phép tịnh tiến theo vectơ \( \overrightarrow{v}\)
là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\)
Lời giải:
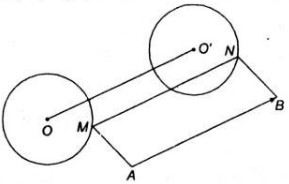
Lấy \(M\) tùy ý. Gọi \({D_{d}}(M) = M'\), \({D_{d'}} (M') = M''\).
Gọi \(M_0,M_1\) lần lượt là giao của \(d\) và \(d'\) với \(MM''\)
Ta có
\( \overrightarrow{MM''}\) =\(\overrightarrow{MM'} + \overrightarrow{M'M''}= 2\overrightarrow{{M_{0}M'}^{}} + 2 \overrightarrow{M'{M_{1}}^{}}\)
\(= 2 \overrightarrow{{M_{0}{M_{1}}^{}}^{}} = 2 \frac{\overrightarrow{v}}{2} = \overrightarrow{v}\)
Vậy \(M'' = {T_{\overrightarrow{v}}} (M) = {D_{d'}}\) \({D_{d}}(M)\), với mọi \(M\)
Do đó phép tịnh tiến theo vectơ \(v\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
