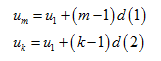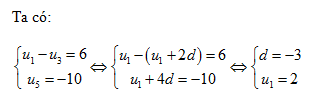
Giải câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao

Bài trước
Bài sau  

Trên tia Ox

Bài 20. Trên tia Ox lấy các điểm A1, A2, …, An, … sao cho với mỗi số nguyên dương n, OAn = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OAn, n = 1, 2, … . Kí hiệu u1 là diện tích của nửa hình tròn đường kính OA1 và với mỗi n ≥ 2, kí hiệu un là diện tích của hình giới hạn bởi nửa đường tròn đường kính OAn – 1 , nửa đường tròn đường kính OAn và tia Ox (h 3.3). Chứng minh rằng dãy số (un) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.

Giải:

Với \(n ≥ 2\) ta có :

\(\eqalign{
& {u_n} = {1 \over 2}\left( {\pi {{OA_n^2} \over 4} - \pi {{OA_{n - 1}^2} \over 4}} \right) \cr
& = {1 \over 8}\pi \left[ {\left( {{n^2} - {{\left( {n - 1} \right)}^2}} \right)} \right] \cr
& = {{\left( {2n - 1} \right)\pi } \over 8}\,\left( {n \ge 2} \right) \cr
& \Rightarrow {u_{n + 1}} - {u_n} = {{2n + 1} \over 8}\pi - {{\left( {2n - 1} \right)} \over 8}\pi = {\pi \over 4},\forall n \ge 2 \cr} \)

Mặt khác

\({u_2} - {u_1} = {{3\pi } \over 8} - {\pi \over 8} = {\pi \over 4}\)

Vậy  \({u_{n + 1}} - {u_n} = {\pi \over 4}\;\forall n \in\mathbb N^*\)

Do đó (un) là cấp số cộng với công sai  \(d = {\pi \over 4}.\)

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 11

Bài học nổi bật nhất

Đề thi lớp 11 mới cập nhật